chevron_left
Zurück zu "Mathematik > x^x Mathematik"
Weiter zu "Mathematik > Primzahlmengen"
chevron_right05.04.2003
Hyperwürfel und Hyperkugeln
Würfel haben neben perfekten Kugeln die Eigenschaft, dass sie zu den einfachsten geometrischen Formen gehören, welche man in n Dimensionen zeichnen oder sich vorstellen kann. Beispielsweise kann man eine Kugel relativ problemlos auf niedrigere Dimensionen "konvertieren", indem man der Oberfläche der Kugel eine Dimension abzieht. So existiert beispielsweise die Vorstellung einer vierdimensionalen Hyperkugel, dessen dreidimensionale Oberfläche unser Universum ist. Zieht man je eine Dimension von diesem Satz ab, so erhält man eine dreidimensionale Kugel mit einer zweidimensionalen Oberfläche - diese Oberfläche kann man immernoch als unser Universum gelten lassen, man muss dabei nur bedenken, dass nun eine Dimension fehlt. Regelmäßigkeiten gelten in diesen Fällen jedoch auch für die fehlende Dimension, wenn klar ist, dass sie auch für die übrigen beiden gelten.
Soviel zur vorzüglichen Eigenschaft von Kugeln. Beliebig-dimensionale Würfel haben den Vorteil, dass man über ein verhältnismäßig einfaches Verfahren zeigen kann, wie ein (n+1)-dimensionaler Würfel aussieht, wenn man einen Würfel mit n Dimensionen zur Verfügung hat. Das hat zwar den Nachteil, dass so ein n-dimensionaler Würfel bei weit über 3 Dimensionen völlig unübersichtlich wird, da wir alle zusätzlichen Dimensionen in unsere wenigen verlegen müssen, aber selbst dann kann man anhand dieses Verfahrens noch zeigen, wie ein Würfel mit einer weiteren Dimension aussehen würde: nämlich genau doppelt so unübersichtlich. :o)
Um zu illustrieren, wie man ein n-dimensionales Würfelobjekt um eine Dimension erweitern kann, fangen wir mit null Dimensionen an. Jegliches Objekt mit null Dimensionen ist ein Punkt.

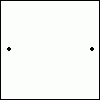
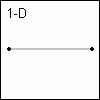
Um nun von null auf eine Dimension zu kommen, kommt noch ein weiterer Punkt hinzu, welcher mit dem ersten durch eine Linie verbunden wird. Anhand dieser Linie kann man nun auf zwei Dimensionen kommen, indem man sie verdoppelt und die unverbundenen Punkte zwischen den zwei Linien verbindet.

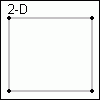
Nun haben wir ein Quadrat, zumindest nahezu :-). Dies kann man nun auf dieselbe Art und Weise auf drei Dimensionen erweitern: man verdoppelt das Vorhandene und verbindet die noch unverbundenen, jeweils gleichen Punkte miteinander. Mit anderen Worten: aus einem Quadrat mach zwei - und dann die gleichen Punkte miteinander verbinden, also zum Beispiel den linken oberen Punkt des ersten Quadrates mit dem linken oberen Punkt des zweiten, und so weiter.
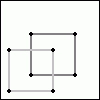
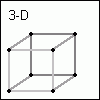
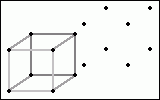
Obwohl wir nur auf die räumliche Sichtweise beschränkt sind, welche ja bekanntlicherweise nur drei Dimensionen hat, können wir aus dem Würfel nun auch einen Hyperwürfel machen. Als Hyperwürfel bezeichnet man einen Würfel mit vier Dimensionen. Wir kopieren einfach wieder das, was wir bereits haben, auf eine beliebige andere Stelle und verbinden schließlich die jeweils gleichen Punkte miteinander.
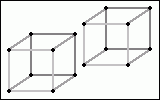
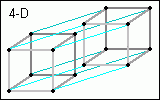
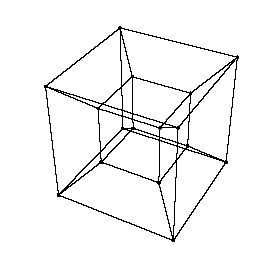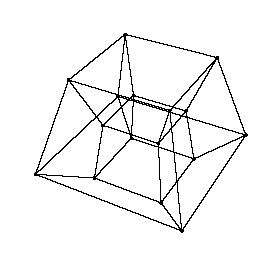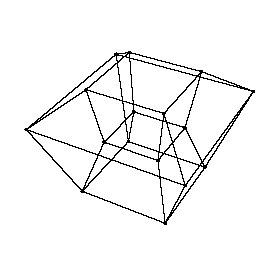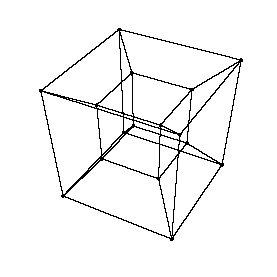
Die Verbindungslinien habe ich nun wegen der Dimensionenzahl, welche ab jetzt größer als 3 ist, anders eingefärbt. Nun haben wir einen Hyperwürfel - die Ursprungsform besteht aus zwei Würfeln, welche einfach an jedem Punkt verbunden werden. Dadurch entstehen noch weitere Würfel, so wie bei 2D-->3D weitere Flächen entstehen, wenn man die noch unverbundenen Punkte zweier Quadrate miteinander verbindet. Nun gibt es für Hyperwürfel ein Bild, welches für uns genauso zulässig ist, wie mein hochqualitativ illustriertes Bild mit den hellblauen Verbindungslinien - dieses sieht aus wie ein kleiner Würfel in einem grossen.
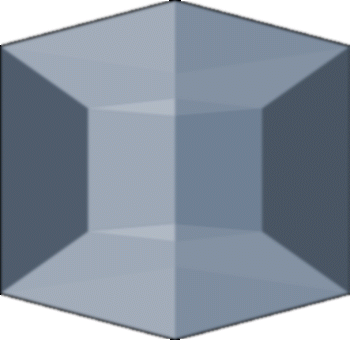
Dies ist eine etwas professioneller gemachte Version eines Hyperwürfels - man erkennt, dass in einem großen Würfel ein etwas kleinerer ist, aus unserer eingeschränkten dreidimensionalen Sicht zumindest. Dieser Hyperwürfel hat nun eine Oberfläche, die aus genau 8 Würfeln mit je drei Dimensionen besteht. Dazu hier eine kleine GIF-Animation, zu der noch zu sagen sei, dass der große Würfel und der kleine Würfel zwei völlig einzelne Würfel dieser Oberfläche darstellen - der große Würfel umfasst zwar in einem der Bilder dieser GIF-Animation den gesamten Hyperwürfel vollständig, er ist jedoch völlig eigenständig und existiert parallel zu dem kleinen Würfel und den 6 Pyramidenstümpfen. Da es eine Eigenschaft des Hyperwürfels ist, dass jede Seite jedes Würfels mit einer Seite irgendeines anderen Würfels verbunden ist, ist dieser äußere Würfel sozusagen notwendig, da die äußeren Seiten der Pyramidenstümpfe sonst außen keine Verbindung zu einem anderen Würfel hätten - so als ob einem gewöhnlichen Würfel irgendwo eine Fläche fehlen würde.
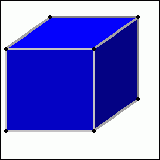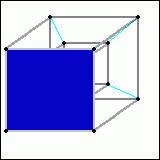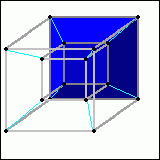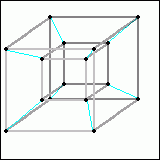
Soviel zum Hyperwürfel. Nun kann man diesen jedoch auch noch erweitern - ab jetzt wirds jedoch deutlich unübersichtlicher. Man kann auch jetzt noch das Vorhandene einfach verdoppeln und an jedem gleichen Punkt verbinden. Da käme in diesem Fall nun so etwas heraus:
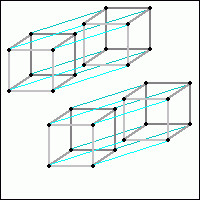
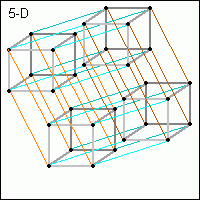
Im rechten Bild sehen wir nun einen fünfdimensionalen Würfel, in drei Dimensionen gezeichnet und auf zwei Dimensionen "heruntergepresst", denn dein Monitor scheint ein ziemlich zweidimensionales Bild zu zeigen :). Die zwei vierdimensionalen Würfel (mit hellblauen Linien verbundene Würfel) sind hier verbunden durch orange Linien. Natürlich kann man dieses Durcheinander noch erweitern...
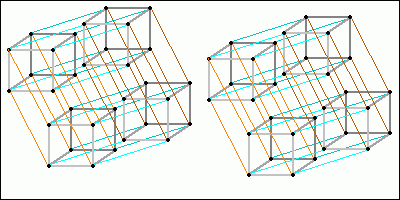
Um es etwas zu vereinfachen, färben wir dieses Bild nun schwarz-weiss und verschieben den rechten 5D-Hyperwürfel etwas nach unten.
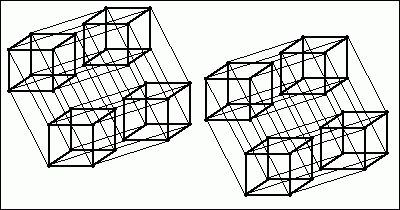
Anschließend können wir beide dieser fünfdimensionalen Hyperwürfel mit farbigen Linien relativ ordentlich miteinander verbinden - wobei ich für die jeweiligen 8 Punkte jedes 3D-Würfels in dem 5D-Würfel eine andere Farbe zum Verbinden nehme, damit man das noch ein wenig unterscheiden kann...
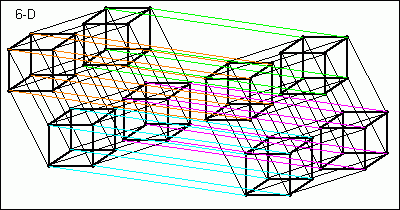
So können wir uns also einen 6D-Hyperwürfel vorstellen - eigentlich Grund genug, um das direkt wieder sein zu lassen, oder? :-)
Man würde anhand dieses Bildes kaum glauben, dass der sechsdimensionale Hyperwürfel noch an jeder Ecke einen rechten Winkel besitzt - dies ist jedoch nur deswegen trügerisch, weil wir 6 Dimensionen irgendwie auf 2 Dimensionen darstellen müssen, was einiges verfälscht. An JEDER Ecke befindet sich jeweils ein 90°-Winkel, könnte man diesen Würfel in 6 Dimensionen betrachten.
Gehen wir erst einmal wieder zurück zu 4 Dimensionen, denn sich diese vorzustellen ist schon schwierig genug. Abgesehen davon gibt es zu diesen noch ein bisschen was zu sagen, was den Hobbymathematiker, der das noch nicht weiss, sicherlich interessieren könnte.
Hier erstmal eine Ansicht eines Hyperwürfels, der sich in der vierten Dimension dreht.
Ewig lang auf die Animation zu starren, bringt in diesem Fall allerdings nicht soviel. Ich weiß nicht mehr, woher ich diese Animation habe, aber der Ersteller hat sich den Spaß erlaubt und einen Sichtwinkel gewählt, von dem aus man nur relativ schlecht nachvollziehen kann, wie sich der Würfel dreht. Nichtsdestotrotz wird dadurch relativ anschaulich gezeigt, dass dieser Würfel unserem dreidimensionalen Verständnis widerspricht.
Wie wir nun oben gesehen haben, ist unsere gängige Vorstellung eines Hyperwürfels "ein kleiner Würfel in einem großen Würfel" - aber wieso? Hier eine Veranschaulichung, wie ein dreidimensionaler Würfel aussehen würde, würde man seinen Schatten in zwei Dimensionen sehen.
Ein kleines Quadrat in einem größeren Quadrat - unsere Vorstellung eines Hyperwürfels sieht ganz ähnlich aus, sie ist also nur der Schatten eines echten Hyperwürfels: ein kleiner Würfel in einem größeren. Dies ist jedoch keinesfalls schlecht oder gar nutzlos - so wie sich ein zweidimensionales Lebewesen anhand des Schattens eines 3D-Würfels vorstellen könnte, wie er logisch und physikalisch funktioniert, so können wir uns anhand des dreidimensionalen Schattens eines Hyperwürfels vorstellen, wie dieser in vier Dimensionen physikalisch/logisch funktioniert. Der innere Würfel stellt sozusagen den Teil des Hyperwürfels dar, das näher an der "Leinwand" liegt - so wie das innere Quadrat auf dem Bild das Ende des Würfels darstellt, das der Leinwand am nächsten ist. Natürlich können wir uns anhand dieses Schattens noch immer kein Bild davon machen, wie nun ein echter Hyperwürfel aussieht - aber mit genug Training kann man es erlernen, sich geistig eine beliebige Hyperwürfel-Drehung vorzustellen.
Ein Hyperwürfel kann, wie ein normaler Würfel auch, ausgeklappt werden. Dies kann man sowohl anhand des Würfels selbst, als auch anhand des Schattens bewerkstelligen. Da wir uns nun vierdimensionale Hyperwürfel nicht direkt vorstellen können, müssen wir auf dessen Schatten zurückgreifen. Weiter unten ist daher ein Video, welches das Aufklappen eines Hyperwürfels zeigt.
Zuerst wird dabei der große Würfel geteilt und unterhalb wieder zusammengesetzt, so dass der gesamte obere Teil des Hyperwürfels freigesetzt ist. Als nächstes können die sechs Pyramidenstümpfe zu normalen Würfeln gemorpht werden, während der mittlere (zunächst kleine) Würfel sich ebenfalls zu einem normal großen Würfel vergrößert. Auf diese Weise erhält man einen sogenannten Tesseract, welcher der ausgeklappte Hyperwürfel ist.
Soviel zur vorzüglichen Eigenschaft von Kugeln. Beliebig-dimensionale Würfel haben den Vorteil, dass man über ein verhältnismäßig einfaches Verfahren zeigen kann, wie ein (n+1)-dimensionaler Würfel aussieht, wenn man einen Würfel mit n Dimensionen zur Verfügung hat. Das hat zwar den Nachteil, dass so ein n-dimensionaler Würfel bei weit über 3 Dimensionen völlig unübersichtlich wird, da wir alle zusätzlichen Dimensionen in unsere wenigen verlegen müssen, aber selbst dann kann man anhand dieses Verfahrens noch zeigen, wie ein Würfel mit einer weiteren Dimension aussehen würde: nämlich genau doppelt so unübersichtlich. :o)
Um zu illustrieren, wie man ein n-dimensionales Würfelobjekt um eine Dimension erweitern kann, fangen wir mit null Dimensionen an. Jegliches Objekt mit null Dimensionen ist ein Punkt.

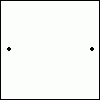

Um nun von null auf eine Dimension zu kommen, kommt noch ein weiterer Punkt hinzu, welcher mit dem ersten durch eine Linie verbunden wird. Anhand dieser Linie kann man nun auf zwei Dimensionen kommen, indem man sie verdoppelt und die unverbundenen Punkte zwischen den zwei Linien verbindet.


Nun haben wir ein Quadrat, zumindest nahezu :-). Dies kann man nun auf dieselbe Art und Weise auf drei Dimensionen erweitern: man verdoppelt das Vorhandene und verbindet die noch unverbundenen, jeweils gleichen Punkte miteinander. Mit anderen Worten: aus einem Quadrat mach zwei - und dann die gleichen Punkte miteinander verbinden, also zum Beispiel den linken oberen Punkt des ersten Quadrates mit dem linken oberen Punkt des zweiten, und so weiter.


Obwohl wir nur auf die räumliche Sichtweise beschränkt sind, welche ja bekanntlicherweise nur drei Dimensionen hat, können wir aus dem Würfel nun auch einen Hyperwürfel machen. Als Hyperwürfel bezeichnet man einen Würfel mit vier Dimensionen. Wir kopieren einfach wieder das, was wir bereits haben, auf eine beliebige andere Stelle und verbinden schließlich die jeweils gleichen Punkte miteinander.



Die Verbindungslinien habe ich nun wegen der Dimensionenzahl, welche ab jetzt größer als 3 ist, anders eingefärbt. Nun haben wir einen Hyperwürfel - die Ursprungsform besteht aus zwei Würfeln, welche einfach an jedem Punkt verbunden werden. Dadurch entstehen noch weitere Würfel, so wie bei 2D-->3D weitere Flächen entstehen, wenn man die noch unverbundenen Punkte zweier Quadrate miteinander verbindet. Nun gibt es für Hyperwürfel ein Bild, welches für uns genauso zulässig ist, wie mein hochqualitativ illustriertes Bild mit den hellblauen Verbindungslinien - dieses sieht aus wie ein kleiner Würfel in einem grossen.

Dies ist eine etwas professioneller gemachte Version eines Hyperwürfels - man erkennt, dass in einem großen Würfel ein etwas kleinerer ist, aus unserer eingeschränkten dreidimensionalen Sicht zumindest. Dieser Hyperwürfel hat nun eine Oberfläche, die aus genau 8 Würfeln mit je drei Dimensionen besteht. Dazu hier eine kleine GIF-Animation, zu der noch zu sagen sei, dass der große Würfel und der kleine Würfel zwei völlig einzelne Würfel dieser Oberfläche darstellen - der große Würfel umfasst zwar in einem der Bilder dieser GIF-Animation den gesamten Hyperwürfel vollständig, er ist jedoch völlig eigenständig und existiert parallel zu dem kleinen Würfel und den 6 Pyramidenstümpfen. Da es eine Eigenschaft des Hyperwürfels ist, dass jede Seite jedes Würfels mit einer Seite irgendeines anderen Würfels verbunden ist, ist dieser äußere Würfel sozusagen notwendig, da die äußeren Seiten der Pyramidenstümpfe sonst außen keine Verbindung zu einem anderen Würfel hätten - so als ob einem gewöhnlichen Würfel irgendwo eine Fläche fehlen würde.

Soviel zum Hyperwürfel. Nun kann man diesen jedoch auch noch erweitern - ab jetzt wirds jedoch deutlich unübersichtlicher. Man kann auch jetzt noch das Vorhandene einfach verdoppeln und an jedem gleichen Punkt verbinden. Da käme in diesem Fall nun so etwas heraus:


Im rechten Bild sehen wir nun einen fünfdimensionalen Würfel, in drei Dimensionen gezeichnet und auf zwei Dimensionen "heruntergepresst", denn dein Monitor scheint ein ziemlich zweidimensionales Bild zu zeigen :). Die zwei vierdimensionalen Würfel (mit hellblauen Linien verbundene Würfel) sind hier verbunden durch orange Linien. Natürlich kann man dieses Durcheinander noch erweitern...

Um es etwas zu vereinfachen, färben wir dieses Bild nun schwarz-weiss und verschieben den rechten 5D-Hyperwürfel etwas nach unten.

Anschließend können wir beide dieser fünfdimensionalen Hyperwürfel mit farbigen Linien relativ ordentlich miteinander verbinden - wobei ich für die jeweiligen 8 Punkte jedes 3D-Würfels in dem 5D-Würfel eine andere Farbe zum Verbinden nehme, damit man das noch ein wenig unterscheiden kann...

So können wir uns also einen 6D-Hyperwürfel vorstellen - eigentlich Grund genug, um das direkt wieder sein zu lassen, oder? :-)
Man würde anhand dieses Bildes kaum glauben, dass der sechsdimensionale Hyperwürfel noch an jeder Ecke einen rechten Winkel besitzt - dies ist jedoch nur deswegen trügerisch, weil wir 6 Dimensionen irgendwie auf 2 Dimensionen darstellen müssen, was einiges verfälscht. An JEDER Ecke befindet sich jeweils ein 90°-Winkel, könnte man diesen Würfel in 6 Dimensionen betrachten.
Gehen wir erst einmal wieder zurück zu 4 Dimensionen, denn sich diese vorzustellen ist schon schwierig genug. Abgesehen davon gibt es zu diesen noch ein bisschen was zu sagen, was den Hobbymathematiker, der das noch nicht weiss, sicherlich interessieren könnte.
Hier erstmal eine Ansicht eines Hyperwürfels, der sich in der vierten Dimension dreht.

Ewig lang auf die Animation zu starren, bringt in diesem Fall allerdings nicht soviel. Ich weiß nicht mehr, woher ich diese Animation habe, aber der Ersteller hat sich den Spaß erlaubt und einen Sichtwinkel gewählt, von dem aus man nur relativ schlecht nachvollziehen kann, wie sich der Würfel dreht. Nichtsdestotrotz wird dadurch relativ anschaulich gezeigt, dass dieser Würfel unserem dreidimensionalen Verständnis widerspricht.
Wie wir nun oben gesehen haben, ist unsere gängige Vorstellung eines Hyperwürfels "ein kleiner Würfel in einem großen Würfel" - aber wieso? Hier eine Veranschaulichung, wie ein dreidimensionaler Würfel aussehen würde, würde man seinen Schatten in zwei Dimensionen sehen.
Ein kleines Quadrat in einem größeren Quadrat - unsere Vorstellung eines Hyperwürfels sieht ganz ähnlich aus, sie ist also nur der Schatten eines echten Hyperwürfels: ein kleiner Würfel in einem größeren. Dies ist jedoch keinesfalls schlecht oder gar nutzlos - so wie sich ein zweidimensionales Lebewesen anhand des Schattens eines 3D-Würfels vorstellen könnte, wie er logisch und physikalisch funktioniert, so können wir uns anhand des dreidimensionalen Schattens eines Hyperwürfels vorstellen, wie dieser in vier Dimensionen physikalisch/logisch funktioniert. Der innere Würfel stellt sozusagen den Teil des Hyperwürfels dar, das näher an der "Leinwand" liegt - so wie das innere Quadrat auf dem Bild das Ende des Würfels darstellt, das der Leinwand am nächsten ist. Natürlich können wir uns anhand dieses Schattens noch immer kein Bild davon machen, wie nun ein echter Hyperwürfel aussieht - aber mit genug Training kann man es erlernen, sich geistig eine beliebige Hyperwürfel-Drehung vorzustellen.
Ein Hyperwürfel kann, wie ein normaler Würfel auch, ausgeklappt werden. Dies kann man sowohl anhand des Würfels selbst, als auch anhand des Schattens bewerkstelligen. Da wir uns nun vierdimensionale Hyperwürfel nicht direkt vorstellen können, müssen wir auf dessen Schatten zurückgreifen. Weiter unten ist daher ein Video, welches das Aufklappen eines Hyperwürfels zeigt.
Zuerst wird dabei der große Würfel geteilt und unterhalb wieder zusammengesetzt, so dass der gesamte obere Teil des Hyperwürfels freigesetzt ist. Als nächstes können die sechs Pyramidenstümpfe zu normalen Würfeln gemorpht werden, während der mittlere (zunächst kleine) Würfel sich ebenfalls zu einem normal großen Würfel vergrößert. Auf diese Weise erhält man einen sogenannten Tesseract, welcher der ausgeklappte Hyperwürfel ist.