chevron_left
Zurück zu "Mathematik > Quadratwurzelnäherung"
Weiter zu "Mathematik > Hyperwürfel und -kugeln"
chevron_right31.03.2003
x^x Mathematik
Das Gebiet der grundsätzlich recht einfach klingenden Formel y=x^x ist ziemlich interessant. Um es für Laien grundlegend zu erklären, steckt da erstmal nicht viel dahinter: 1^1=1, 2^2=4, 3^3=27, 4^4=256 und so fort. Wie jedoch könnte man eine Umkehrung für diese Rechenoperation finden? Auf welchem Weg könnte man von der 256 auf die 4 schließen, von der 27 auf die 3, und so weiter? Ich habe bisher nur eine Möglichkeit dazu gefunden, die man auf beinahe jedem Taschenrechner durchführen kann:
Diese Formel liefert beliebig genaue Ergebnisse, es seidenn, der x-Wert ist größer als die irrationale Zahl e, welche mit 2,718281828 beginnt. Sobald das x, welches man vorher nicht kennt, größer ist als e, bekommt man nicht nur ein Ergebnis, sondern sogar 2 - lustigerweise wechselt der Taschenrechner dann immer zwischen den zwei Ergebnissen hin und her. Man kann erkennen, ob dies der Fall sein wird, wenn die Zahl y, welche man ja kennt, größer als etwa 15.15 ist, denn e^e = 15.15426..., welche sozusagen die Grenze bei dieser Näherung zu x darstellt. Nun bekommt man, wie bereits erwähnt, nicht nur ein Ergebnis, sondern gleich zwei - je größer das y ist, dessen x man berechnen will, desto mehr geht der eine Wert gegen 1 und der andere Wert gegen y. Bezeichnen wir diese beiden neuen Zahlen nun als a und b, um die Übersicht zu behalten. Nun haben diese beiden Zahlen interessante Eigenschaften, denn a^b liefert genau das gleiche Ergebnis wie b^a, nämlich exakt y. Mathematisch kann man also sagen:
Jetzt werden einige etwas eingefleischtere Leute sagen: halt mal, was ist denn, wenn x GENAU e ist? Das Problem in diesem Fall ist: das geht überhaupt nicht, da e unendlich viele Nachkommastellen hat, sie ist irrational. In endlicher Zeit kann man nur endlich viele Nachkommastellen von e errechnen, so dass man nur von mehr oder weniger als e sprechen kann, niemals jedoch GENAU von e - eine der verwirrenden Eigenschaften irrationaler Zahlen. Dass wir die Zahl als "e" bezeichnen, bedeutet noch lange nicht, dass wir sie vollständig kennen - nur über eine vollständig bekannte Zahl kann man sagen, dass sie größer, kleiner oder gleich einer anderen Zahl ist. Bei einer nicht vollständig bekannten Zahl herrscht immer eine gewisse Ungewissheit - bei unendlich vielen Nachkommastellen herrscht diese Ungewissheit unendlich lange, es kann also rechnerisch keine Zahl geben, die genau so groß ist, wie das, was wir Euler'sche Zahl nennen. Eventuell wird der Fall x=e irgendwann auf irgendeine völlig andere Weise herleitbar sein - derzeit scheint es jedoch nicht bestimmbar zu sein, ob der Fall x=e mit zur Kategorie x>e gehört oder ob für diesen Spezialfall mit unendlich vielen Nachkommastellen etwas völlig unerwartetes der Fall ist. In jedem Fall stellt e den Grenzwert dar, oberhalb welchem a und b existieren.
Ein Beispiel für ein a und ein b sind die einzigen ganzen Zahlen, die in diesem Teilbereich vorkommen: a=2, b=4. 2^4 und 4^2 ergeben nämlich beide 16, das x liegt irgendwo bei etwa 2.745368024, wobei sich das meines derzeitigen Wissens nach nur mit der "probieren-und-immer-weiter-annähern"-Methode beliebig genau gelöst werden kann, wenn x größer als e ist - das geht natürlich auch über einen Algorithmus, wenn man so einen programmieren möchte.
Hier ein Graph, in welchem x, y, a und b bis y=18.5 sichtbar werden:
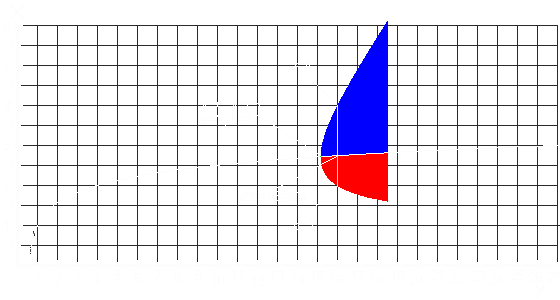
Die weiße Linie steht nach oben hin für das x, welches jeweils notwendig ist, damit x^x genau y ergibt, welches durch die weiße Linie von links nach rechts gekennzeichnet wird. Sobald x größer als die Zahl e (2,718...) ist bzw. sobald y größer als e^e (ca. 15,154) ist, tauchen auch die zwei Variablen a und b auf, a ist größer als x und geht gegen y während b jeweils kleiner als x ist und gegen 1 konvergiert. Für diese Zahlen gilt: a^b und b^a ergeben beide dasselbe Ergebnis, nämlich y, also genau das, was auch bei x^x rauskommt. Für jedes y gibt es nur exakt eine einzige Kombination von a und b, sämtliche anderen Zahlen würden vielleicht bei a^b das richtige Ergebnis y liefern, bei b^a würde jedoch etwas anderes herauskommen - oder umgedreht, je nachdem. Das a wird in dem Graphen gekennzeichnet durch den jeweils obersten Punkt des blauen Bereiches - der jeweils unterste Punkt des roten Bereiches steht für b.
Ich vermute, dass a und b auch existieren, wenn x kleiner als e ist - nur dass sie dann nicht zu den reellen Zahlen, sondern zu den komplexen Zahlen gehören. Wer dazu Lust hat, möge versuchen, es zu beweisen. :)
X0 > 0
X1 = X0√y
(Die X0-te Wurzel von y)
X2 = X1√y
X3 = X2√y
...
X1 = X0√y
(Die X0-te Wurzel von y)
X2 = X1√y
X3 = X2√y
...
Diese Formel liefert beliebig genaue Ergebnisse, es seidenn, der x-Wert ist größer als die irrationale Zahl e, welche mit 2,718281828 beginnt. Sobald das x, welches man vorher nicht kennt, größer ist als e, bekommt man nicht nur ein Ergebnis, sondern sogar 2 - lustigerweise wechselt der Taschenrechner dann immer zwischen den zwei Ergebnissen hin und her. Man kann erkennen, ob dies der Fall sein wird, wenn die Zahl y, welche man ja kennt, größer als etwa 15.15 ist, denn e^e = 15.15426..., welche sozusagen die Grenze bei dieser Näherung zu x darstellt. Nun bekommt man, wie bereits erwähnt, nicht nur ein Ergebnis, sondern gleich zwei - je größer das y ist, dessen x man berechnen will, desto mehr geht der eine Wert gegen 1 und der andere Wert gegen y. Bezeichnen wir diese beiden neuen Zahlen nun als a und b, um die Übersicht zu behalten. Nun haben diese beiden Zahlen interessante Eigenschaften, denn a^b liefert genau das gleiche Ergebnis wie b^a, nämlich exakt y. Mathematisch kann man also sagen:
x^x = y = a^b = b^a für x>e
x = a = b für x<e
x = a = b für x<e
Jetzt werden einige etwas eingefleischtere Leute sagen: halt mal, was ist denn, wenn x GENAU e ist? Das Problem in diesem Fall ist: das geht überhaupt nicht, da e unendlich viele Nachkommastellen hat, sie ist irrational. In endlicher Zeit kann man nur endlich viele Nachkommastellen von e errechnen, so dass man nur von mehr oder weniger als e sprechen kann, niemals jedoch GENAU von e - eine der verwirrenden Eigenschaften irrationaler Zahlen. Dass wir die Zahl als "e" bezeichnen, bedeutet noch lange nicht, dass wir sie vollständig kennen - nur über eine vollständig bekannte Zahl kann man sagen, dass sie größer, kleiner oder gleich einer anderen Zahl ist. Bei einer nicht vollständig bekannten Zahl herrscht immer eine gewisse Ungewissheit - bei unendlich vielen Nachkommastellen herrscht diese Ungewissheit unendlich lange, es kann also rechnerisch keine Zahl geben, die genau so groß ist, wie das, was wir Euler'sche Zahl nennen. Eventuell wird der Fall x=e irgendwann auf irgendeine völlig andere Weise herleitbar sein - derzeit scheint es jedoch nicht bestimmbar zu sein, ob der Fall x=e mit zur Kategorie x>e gehört oder ob für diesen Spezialfall mit unendlich vielen Nachkommastellen etwas völlig unerwartetes der Fall ist. In jedem Fall stellt e den Grenzwert dar, oberhalb welchem a und b existieren.
Ein Beispiel für ein a und ein b sind die einzigen ganzen Zahlen, die in diesem Teilbereich vorkommen: a=2, b=4. 2^4 und 4^2 ergeben nämlich beide 16, das x liegt irgendwo bei etwa 2.745368024, wobei sich das meines derzeitigen Wissens nach nur mit der "probieren-und-immer-weiter-annähern"-Methode beliebig genau gelöst werden kann, wenn x größer als e ist - das geht natürlich auch über einen Algorithmus, wenn man so einen programmieren möchte.
Hier ein Graph, in welchem x, y, a und b bis y=18.5 sichtbar werden:

Die weiße Linie steht nach oben hin für das x, welches jeweils notwendig ist, damit x^x genau y ergibt, welches durch die weiße Linie von links nach rechts gekennzeichnet wird. Sobald x größer als die Zahl e (2,718...) ist bzw. sobald y größer als e^e (ca. 15,154) ist, tauchen auch die zwei Variablen a und b auf, a ist größer als x und geht gegen y während b jeweils kleiner als x ist und gegen 1 konvergiert. Für diese Zahlen gilt: a^b und b^a ergeben beide dasselbe Ergebnis, nämlich y, also genau das, was auch bei x^x rauskommt. Für jedes y gibt es nur exakt eine einzige Kombination von a und b, sämtliche anderen Zahlen würden vielleicht bei a^b das richtige Ergebnis y liefern, bei b^a würde jedoch etwas anderes herauskommen - oder umgedreht, je nachdem. Das a wird in dem Graphen gekennzeichnet durch den jeweils obersten Punkt des blauen Bereiches - der jeweils unterste Punkt des roten Bereiches steht für b.
Ich vermute, dass a und b auch existieren, wenn x kleiner als e ist - nur dass sie dann nicht zu den reellen Zahlen, sondern zu den komplexen Zahlen gehören. Wer dazu Lust hat, möge versuchen, es zu beweisen. :)