Primzahlzwillinge, die mysteriösen Primzahlpartner, haben sich in der Mathematik schon vor Jahrtausenden schnell zu einem beliebten Mathematikzweig entwickelt. 11 und 13 sind Zwillinge, 17 und 19 ebenfalls, genauso wie 29 und 31, etc. - also jeweils zwei Primzahlen, deren Differenz 2 beträgt. Leider sind bis zum heutigen Tage nur wenig nützliche Fakten über Primzahlzwillinge bekannt - sie scheinen nur sporadisch und ohne jegliches Muster vorzukommen.

Grund genug für mich, etwas Zeit aufzuwenden um möglicherweise etwas herauszufinden. Gesagt, getan - während der Nacht vom 24.11.2003 auf den 25.11.2003 habe ich eine interessante Regelmäßigkeit unter den Primzahlzwillingen entdeckt. Leider konnte ich diese Regelmäßigkeit aufgrund mangelhafter Software nur im Ansatz verfolgen, weswegen ich für jedwede Hilfe, die geleistet wurde und evtl. noch geleistet werden wird, sehr sehr dankbar bin.

1.1.a.) unter den ersten 10 Zahlen gibt es 4 Primzahlen
1.1.b.) unter den ersten 10 Primzahlen gibt es 4 Primzahlzwillinge

2.1.a.) unter den ersten 100 Zahlen gibt es 25 Primzahlen
2.1.b.) unter den ersten 100 Primzahlen gibt es 25 Primzahlzwillinge

3.1.a.) unter den ersten 1000 Zahlen gibt es 168 Primzahlen
3.1.b.) unter den ersten 1000 Primzahlen gibt es 174 Primzahlzwillinge

4.1.a.) unter den ersten 10000 Zahlen gibt es 1229 Primzahlen
4.1.b.) unter den ersten 10000 Primzahlen gibt es 1270 Primzahlzwillinge

Danke an Henrik Schulz für 5.1:
5.1.a.) unter den ersten 100000 Zahlen gibt es 9592 Primzahlen
5.1.b.) unter den ersten 100000 Primzahlen gibt es 10250 Primzahlzwillinge

Danke an Eugen Bauhof für 6.1 - 7.3:
6.1.a.) unter den ersten 1000000 Zahlen gibt es 78498 Primzahlen
6.1.b.) unter den ersten 1000000 Primzahlen gibt es 86027 Primzahlzwillinge

6.2.a.) unter den ersten 2000000 Zahlen gibt es 148933 Primzahlen
6.2.b.) unter den ersten 2000000 Primzahlen gibt es 163766 Primzahlzwillinge

6.3.a.) unter den ersten 3000000 Zahlen gibt es 216816 Primzahlen
6.3.b.) unter den ersten 3000000 Primzahlen gibt es 239003 Primzahlzwillinge

6.4.a.) unter den ersten 4000000 Zahlen gibt es 283146 Primzahlen
6.4.b.) unter den ersten 4000000 Primzahlen gibt es 312703 Primzahlzwillinge

6.5.a.) unter den ersten 5000000 Zahlen gibt es 348513 Primzahlen
6.5.b.) unter den ersten 5000000 Primzahlen gibt es 385375 Primzahlzwillinge

6.6.a.) unter den ersten 6000000 Zahlen gibt es 412849 Primzahlen
6.6.b.) unter den ersten 6000000 Primzahlen gibt es 457399 Primzahlzwillinge

6.7.a.) unter den ersten 7000000 Zahlen gibt es 476648 Primzahlen
6.7.b.) unter den ersten 7000000 Primzahlen gibt es 528528 Primzahlzwillinge

6.8.a.) unter den ersten 8000000 Zahlen gibt es 539777 Primzahlen
6.8.b.) unter den ersten 8000000 Primzahlen gibt es 599296 Primzahlzwillinge

6.9.a.) unter den ersten 9000000 Zahlen gibt es 602489 Primzahlen
6.9.b.) unter den ersten 9000000 Primzahlen gibt es 669294 Primzahlzwillinge

7.1.a.) unter den ersten 10000000 Zahlen gibt es 664579 Primzahlen
7.1.b.) unter den ersten 10000000 Primzahlen gibt es 738597 Primzahlzwillinge

7.2.a.) unter den ersten 11000000 Zahlen gibt es 726517 Primzahlen
7.2.b.) unter den ersten 11000000 Primzahlen gibt es 807787 Primzahlzwillinge

7.3.a.) unter den ersten 12000000 Zahlen gibt es 788060 Primzahlen
7.3.b.) unter den ersten 12000000 Primzahlen gibt es 876670 Primzahlzwillinge

Die Häufigkeit der Primzahlzwillinge innerhalb der Primzahlen scheint also eng mit der Häufigkeit der Primzahlen in den Ganzen Zahlen (1, 2, 3, etc.) zusammenzuhängen. Dies sind nun sehr grundlegende, zahlentheoretische Fakten - also, habe ich mir gedacht, verfolge ich das ebenso grundlegend und zahlentheoretisch weiter. Die allererste Näherungsformel, die es jemals gab, mit welcher man die Anzahl der Primzahlen abschätzen kann, ist x/ln(x). Diese gibt etwa an, wie viele Primzahlen zwischen 1 und x liegen. Umgekehrt ergibt die Formel x*ln(x) annähernd die x-te Primzahl. Da x*ln(x) als Umkehrung zu x/ln(x) zu verstehen ist, kann man dies wohl auch andersherum benutzen: damit muesste man abschätzen können, wie viele Zahlen nötig sind, damit sie x Primzahlzwillinge enthalten. Um dies zu bewerkstelligen, ist jedoch noch etwas mehr nötig, wie man an folgender Tabelle sieht:

x Ganze Zahlen enthalten -->	y Primzahlen enthalten -->	z Primzahlzwillinge
x	y = x / ln(x)	z = [x / ln(x)] / ln[x / ln(x)]
x = y * ln(x)	y	z = y / ln(y)
x = z * ln(y) * ln(x)	y = z * ln(y)	z

Die pink eingefärbten Formeln in der linken unteren Ecke der Tabelle sind so leider nicht lösbar, wenn man nicht gerade die Nadel im Heuhaufen suchen will. Nehmen wir als Beispiel y = z * ln(y). Wir müssten, um y als Lösung zu erhalten, y bereits kennen - da dies ein Widerspruch ist, ist es nicht ganz so einfach. Deswegen müssen wir irgendwie versuchen, über Umwege y zu berechnen oder zumindest abzuschätzen. Mein Ansatz ist nun, ln(y) anhand von ln(z) abzuschätzen. Wie groß ist der Unterschied zwischen beiden Zahlen und wodurch könnte man ihn ausgleichen?

Hier nun meine Überlegungen:

1a.) 100 / ln(100) = 21,7147
1b.) 21,7147 * ln(21,7147) = 66,8377
1c.) 21,7147 * ln(66,8377 * √2) = 98,7768

2a.) 1000 / ln(1000) = 144,7648
2b.) 144,7648 * ln(144,7648) = 720,2210
2c.) 144,7648 * ln(720,2210 * √2) = 1002,6603

3a.) 10000 / ln(10000) = 1085,7362
3b.) 1085,7362 * ln(1085,7362) = 7589,3108
3c.) 1085,7362 * ln(7589,3108 * √2) = 10076,7933

4a.) 100000 / ln(100000) = 8685,8896
4b.) 8685,8896 * ln(8685,8896) = 78776,2861
4c.) 8685,8896 * ln(78776,2861 * √2) = 100938,21

Das ist meiner Meinung nach erstmal genau genug - also kann man folgende Näherungsformel wagen:

a.) x / ln(x) = n
b.) n * ln(n) = m
c.) n * ln(m * √2) ~ x
d.) n * ln(n * ln(n) * √2) ~ x

Die Wurzel 2 ist dabei nur ein Näherungsfaktor - ansonsten könnte man nämlich diese Näherung immer weiter verschachteln und sie auf diesem Weg immer akkurater machen. Das würde dann so aussehen: x = n * ln(n * ln(n * ln(n * ln(n * ...))))

Da es hierbei jedoch grundlegend nur um Abschätzungen geht, sollte es einfach gehalten bleiben. Nun können wir das x von x/ln(x) abschätzen und so die obrige Tabelle etwas verändern, damit sie für unsere Zwecke nützlicher wird. Wie man in folgender Tabelle sieht, ist es trotz der starken Vereinfachung immernoch extrem, wenn man von z auf x schliessen möchte.

x Ganze Zahlen enthalten -->	y Primzahlen enthalten -->	z Primzahlzwillinge
x	y = x / ln(x)	z = [x / ln(x)] / ln[x / ln(x)]
x = y * ln(y * ln(y) * √2)	y	z = y / ln(y)
x = z * ln(y) * ln(y * ln(y) * √2)	y = z * ln(z * ln(z) * √2)	z
x = z * ln(z * ln(z * ln(z) * √2)) * ln(z * ln(z * ln(z) * √2)) * ln(z * ln(z * ln(z) * √2) * √2)

Würde man die Formel für x in der dritten Zeile dieser Tabelle ganz ausschreiben, so würde die pink gefärbte Formel dabei entstehen. Würde man dies noch vereinfachen wollen, so müsste man die ganze Näherung ungenauer machen. Aus diesem Grund ist es ratsam, zuerst

y = z * ln(z * ln(z) * √2)

auszurechnen und anschließend y und z in die Formel

x = z * ln(y) * ln(y * ln(y) * √2)

zu übertragen.

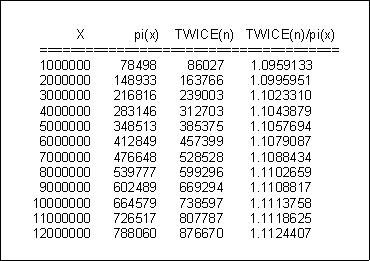
Hier noch eine Tabelle von Eugen Bauhof, welche aufzeigt, dass der Faktor, der Primzahlmenge mit Zwillingsmenge verbindet, offenbar konvergiert, also im Unendlichen einen ganz bestimmten Wert annimmt. Ähnlich wie x/ln(x) die Anzahl der Primzahlen unter den Ganzen Zahlen annähernd bestimmt, würde n * x/ln(x) die Anzahl der Primzahlzwillinge unter den Primzahlen annähernd bestimmen. Ich bin gespannt, wie groß dieser Faktor genau ist! Hier die Tabelle: