30.03.2003
Quadratwurzelnäherung
Ich habe lange aus Spaß an der Sache mit Formeln rumgespielt und wende auch heute noch so manche algebraische Umstellung an, die wohl nicht wirklich als äquivalent zu bezeichnen ist. Klar, sehr oft kommt dabei nur Unsinn heraus, jedoch gibt es auch Ausnahmefälle, so dass man durch einen kleinen Fehler in der Umstellung zu einer völlig anderen Formel gelangt, die grundsätzlich für das Gleiche gut ist, jedoch einen etwas anderen Zweck erfüllt. Irgendwann kam ich auf die Idee, dass ich Wurzeln nicht immer mit Taschenrechnern ausrechnen will, sondern dass ich sie auch im Kopf wenigstens annähernd richtig berechnen können möchte. Angefangen haben meine Bemühungen mit einer nicht ganz optimalen Formel, in welcher neben der zu suchenden Zahl noch genau zwei Quadratzahlen (a^2 und b^2, a und b als Element der ganzen Zahlen (1, 2, 3, ...)) nötig sind - die eine niedriger als die Gesuchte, die andere höher - welche sozusagen als Orientierung dienten, um von einer dazwischenliegenden Zahl die Wurzel berechnen zu können. Die Formel der gesuchten Wurzel w war zu der Zeit:
w = √a + (x - a)/(b - a)
Bald darauf ist mir aufgefallen, dass der Teil (b-a) immer relativ zu a umformuliert werden kann, so dass die Variable b überflüssig wird. Eins plus dem Doppelten der Wurzel aus a entsprach genau b-a, wodurch die Formel leicht abgeändert werden konnte. Nun wollte ich die Formel jedoch so einfach wie nur möglich halten, so dass ich das "1+" im Nenner des Bruches einfach mal weggelassen habe, was eine der nicht ganz äquivalenten Umformungen darstellt:
w = √a + (x - a)/(2*√a)
Der Rechenfehler der Näherungsformel wurde dadurch zwar größer, die Formel war nun jedoch insgesamt einfacher.
Einige Tage danach ist mir aufgefallen, dass die wahre Wurzel in jedem Fall irgendwo zwischen den beiden obigen Wurzelnäherungen liegt - ich könnte also beide Formeln verbinden und deren Durchschnittswert nehmen, was die Berechnung letztlich um einiges genauer machen müsste. Durch die folgende Formel hatte ich es zumindest erreicht, dass die erste Nachkommastelle meist korrekt war, die zweite Nachkommastelle in einigen Fällen ebenfalls:
w = [2*√a + (x - a)/(b - a) + (x - a)/(2*√a)] / 2
Nun hatte ich wieder zwei zusätzliche Orientierungsvariablen - mir ist es nicht sofort wieder eingefallen, aber hatte ich nicht mal was davon erwähnt, dass (b-a) relativ zu a formuliert werden kann? Das entspricht doch prinzipiell genau dem Nenner des anderen Bruchs, nur dass bei dem ersten Bruch einfach 1 dazugezählt wird. Wir erhalten also:
w = [2*√a + (x - a)/(2*√a+1) + (x - a)/(2*√a)] / 2
Nun können wir die 2 am Ende der Formel, die in korrekter mathematischer Formulierung unterhalb des Bruchstriches des Termes innerhalb der eckigen Klammern stehen müsste, auf alle drei Summanden einzeln anwenden:
Nun stellt sich die Frage, ob man diese genaue UND leider recht lange Formel nicht irgendwie verkürzen kann. Hier kam nun eine meiner bewehrten Probier-Methoden zum Einsatz, welche die Gleichung nach langem Herumprobieren wie folgt änderte:
w = √a + 4(x - a)/(8*√a + 2)
Und selbstverständlich kann man hier prima kürzen...
w = √a + (x - a)/(2*√a + 0.5)
Schöne kurze Formel, aber warum zum Teufel muss da +0.5 stehen, damit sie so genau ist? Wäre vielleicht 0.33 oder 0.67 genauer? Ich habe diese Zahl nun z genannt, stehend für Zusatz, und habe mir schliesslich eine Liste gemacht, mit welchem z eine Wurzelnäherung jeweils am genauesten ist. Das erstaunliche dabei war: welche Zahl man für die 0.5 einsetzt, spielt ueberhaupt gar keine Rolle, solange man das dadurch entstehende Ergebnis an die Stelle der 0.5 einsetzt und das ganze nochmals rechnet. Das kann man sogar öfter machen und so letztlich die Wurzel beliebig genau ausrechnen.
Durch viel Herumprobierei, welche gut 4 DIN-A4-Seiten verschlungen hat, ist es mir schliesslich gelungen, diese so genannte Iteration (schrittweise Näherung) noch erheblich zu vereinfachen - sie beinhaltet nun keine Wurzeln mehr und lautet:
Z1 = 1 + (x - 1)/(Z0 + 1)
Das wiederrum, obgleich schon sehr einfach, kann man noch weiter vereinfachen. Zu meiner Schande muss ich gestehen, dass ich mir die Formel fast 2 Jahre lang nicht mehr angeschaut habe - anschließend sah ich auf Anhieb, dass es noch einfacher gehen muss. Das Ergebnis war folgendes:
Zn+1 = (Zn + x)/(Zn + 1)
Eine wunderbar einfache Iteration zur Wurzelberechnung - sie gilt zwar nur zur Berechnung von zweiten Wurzeln, also von Quadratwurzeln, beinhaltet gegenüber der Newton'schen Iteration beliebiger Wurzeln lediglich die vier Grundrechenarten. Die Newton'sche Iteration beinhaltet, wie ich später herausfand, einmal die Potenz (n-1) und lautet komplizierterweise wie folgt:
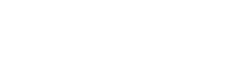
Gegenüber der simplen Iteration für zweite Wurzeln ist die Newton'sche Iteration reichlich kompliziert, wie ich finde. Ausgleichend ist sie in der Lage, jede beliebige Wurzel von jeder beliebigen Zahl beliebig genau zu iterieren.
Was mich jetzt noch interessieren würde: kann man meine Iteration irgendwie aus der von Newton herleiten? Vielleicht ist es möglich, vielleicht gehen die Iterationen jedoch auch verschiedene Wege - wer die Herleitung versuchen oder beweisen möchte, dass die Iterationen unterschiedlich sind, möge das tun. Sofern widerspruchsfrei, nehme ich die Herleitung, den Beweis oder einen widerlegenden Beweis jederzeit hier auf.
Was das Kopfrechnen von Wurzeln angeht, so habe ich mich letztlich für die einfachste Ein-Schritt-Formel entschieden:
w = √a + (x - a)/(2*√a)
Wer jetzt damit beginnt, diese Formel auswendig zu lernen, wird schon bald merken, dass sie sich viel einfacher merken lässt, als man anfänglich meint. Ich demonstriere es anhand eines Beispiels: will man Wurzel 19 berechnen, nimmt man sich die nächstbeste Quadratzahl, die 16. Da Wurzel 19 zwischen Wurzel 16 (4^2) und Wurzel 25 (5^2) liegt, weiss man, dass sie vor dem Komma eine 4 haben muss, wofür die Wurzel dieser nächstbesten Quadratzahl, in diesem Fall die 16, herhält. Nun noch die Nachkommastellen, und da ist ein simpler Bruch gut - wie weit ist 19 von 16 entfernt? Genau um 3 Zahlen, das stellen wir über den Bruchstrich. Nun noch einen willkürlich klingenden Wert: das Doppelte der nächstbesten Wurzel 16, in diesem Fall also 8, stellen wir unter den Bruchstrich. Wir haben also in etwa 4 + 3/8, was man so als Lösung stehenlassen kann, wenn man den Bruch nicht in eine Dezimalzahl umwandeln möchte. Als Dezimalzahl lautet der Bruch 4,375 - die wahre Wurzel aus 19 lautet 4,3589..., womit wir diese schon sehr gut getroffen haben.
Um noch ein Beispiel zu nennen, wie ist die Wurzel aus 29? Die nächstbesten Quadratzahlen sind 25 und 36, nehmen wir hierbei einfach mal die größere - um zu zeigen, dass es damit genauso gut geht. Die Wurzel der nächsthöheren ist 6, die Zahl vor dem Komma der gesuchten Wurzel muss somit um eins niedriger sein, also 5. Wie weit is 29 von 36 entfernt? Genau, 29 ist um 7 kleiner. Nun wieder das Doppelte der Wurzel aus der nächstbesten Quadratzahl, also 2*6, das macht 12. Die Wurzel lautet also in etwa 6 + (-7)/12 oder auch 6 - 7/12, was in etwa zwischen 5,4 und 5,5 liegt. Die wahre Wurzel ist nun 5,385..., was damit zusammenhängt, dass wir eine nächstbeste Quadratzahl genommen haben, die etwas weiter entfernt war, nämlich um 7 Zahlen. Die wirklich nächste wäre die 25 gewesen, die nur um 4 Zahlen entfernt ist. Das Ergebnis damit wäre 5 + 4/10, also 5,4 - das ist ein genaueres Ergebnis, was prinzipiell einer Rundung der wahren Wurzel entspricht. Je weiter sich die nächstbeste Quadratzahl also entfernt, desto größer wird der Näherungsfehler - in den meisten Fällen jedoch sollte das zu verkraften sein, wenn man nicht gerade die ersten 100 Nachkommastellen einer Quadratwurzel exakt berechnen möchte. :-) Und in jenem Fall gibt es die bereits genannte, einfachste Quadratwurzel-Iteration der Welt mit x als für die gesuchte Wurzel stehende Variable:
Zn+1 = (Zn + x)/(Zn + 1)
w = √a + (x - a)/(b - a)
Bald darauf ist mir aufgefallen, dass der Teil (b-a) immer relativ zu a umformuliert werden kann, so dass die Variable b überflüssig wird. Eins plus dem Doppelten der Wurzel aus a entsprach genau b-a, wodurch die Formel leicht abgeändert werden konnte. Nun wollte ich die Formel jedoch so einfach wie nur möglich halten, so dass ich das "1+" im Nenner des Bruches einfach mal weggelassen habe, was eine der nicht ganz äquivalenten Umformungen darstellt:
w = √a + (x - a)/(2*√a)
Der Rechenfehler der Näherungsformel wurde dadurch zwar größer, die Formel war nun jedoch insgesamt einfacher.
Einige Tage danach ist mir aufgefallen, dass die wahre Wurzel in jedem Fall irgendwo zwischen den beiden obigen Wurzelnäherungen liegt - ich könnte also beide Formeln verbinden und deren Durchschnittswert nehmen, was die Berechnung letztlich um einiges genauer machen müsste. Durch die folgende Formel hatte ich es zumindest erreicht, dass die erste Nachkommastelle meist korrekt war, die zweite Nachkommastelle in einigen Fällen ebenfalls:
w = [2*√a + (x - a)/(b - a) + (x - a)/(2*√a)] / 2
Nun hatte ich wieder zwei zusätzliche Orientierungsvariablen - mir ist es nicht sofort wieder eingefallen, aber hatte ich nicht mal was davon erwähnt, dass (b-a) relativ zu a formuliert werden kann? Das entspricht doch prinzipiell genau dem Nenner des anderen Bruchs, nur dass bei dem ersten Bruch einfach 1 dazugezählt wird. Wir erhalten also:
w = [2*√a + (x - a)/(2*√a+1) + (x - a)/(2*√a)] / 2
Nun können wir die 2 am Ende der Formel, die in korrekter mathematischer Formulierung unterhalb des Bruchstriches des Termes innerhalb der eckigen Klammern stehen müsste, auf alle drei Summanden einzeln anwenden:
| [1] | 2*√a : 2 | = | √a |
| [2] | (x - a)/(2*√a + 1) : 2 | = | (x - a)/(4*√a + 2) |
| [3] | (x - a)/(2*√a) | = | (x - a)/(4*√a) |
| --> | w | = | [1] + [2] + [3] |
| --> | w | = | √a + (x - a)/(4*√a) + (x - a)/(4*√a + 2) |
Nun stellt sich die Frage, ob man diese genaue UND leider recht lange Formel nicht irgendwie verkürzen kann. Hier kam nun eine meiner bewehrten Probier-Methoden zum Einsatz, welche die Gleichung nach langem Herumprobieren wie folgt änderte:
w = √a + 4(x - a)/(8*√a + 2)
Und selbstverständlich kann man hier prima kürzen...
w = √a + (x - a)/(2*√a + 0.5)
Schöne kurze Formel, aber warum zum Teufel muss da +0.5 stehen, damit sie so genau ist? Wäre vielleicht 0.33 oder 0.67 genauer? Ich habe diese Zahl nun z genannt, stehend für Zusatz, und habe mir schliesslich eine Liste gemacht, mit welchem z eine Wurzelnäherung jeweils am genauesten ist. Das erstaunliche dabei war: welche Zahl man für die 0.5 einsetzt, spielt ueberhaupt gar keine Rolle, solange man das dadurch entstehende Ergebnis an die Stelle der 0.5 einsetzt und das ganze nochmals rechnet. Das kann man sogar öfter machen und so letztlich die Wurzel beliebig genau ausrechnen.
Durch viel Herumprobierei, welche gut 4 DIN-A4-Seiten verschlungen hat, ist es mir schliesslich gelungen, diese so genannte Iteration (schrittweise Näherung) noch erheblich zu vereinfachen - sie beinhaltet nun keine Wurzeln mehr und lautet:
Z1 = 1 + (x - 1)/(Z0 + 1)
Das wiederrum, obgleich schon sehr einfach, kann man noch weiter vereinfachen. Zu meiner Schande muss ich gestehen, dass ich mir die Formel fast 2 Jahre lang nicht mehr angeschaut habe - anschließend sah ich auf Anhieb, dass es noch einfacher gehen muss. Das Ergebnis war folgendes:
Zn+1 = (Zn + x)/(Zn + 1)
Eine wunderbar einfache Iteration zur Wurzelberechnung - sie gilt zwar nur zur Berechnung von zweiten Wurzeln, also von Quadratwurzeln, beinhaltet gegenüber der Newton'schen Iteration beliebiger Wurzeln lediglich die vier Grundrechenarten. Die Newton'sche Iteration beinhaltet, wie ich später herausfand, einmal die Potenz (n-1) und lautet komplizierterweise wie folgt:
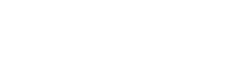
Gegenüber der simplen Iteration für zweite Wurzeln ist die Newton'sche Iteration reichlich kompliziert, wie ich finde. Ausgleichend ist sie in der Lage, jede beliebige Wurzel von jeder beliebigen Zahl beliebig genau zu iterieren.
Was mich jetzt noch interessieren würde: kann man meine Iteration irgendwie aus der von Newton herleiten? Vielleicht ist es möglich, vielleicht gehen die Iterationen jedoch auch verschiedene Wege - wer die Herleitung versuchen oder beweisen möchte, dass die Iterationen unterschiedlich sind, möge das tun. Sofern widerspruchsfrei, nehme ich die Herleitung, den Beweis oder einen widerlegenden Beweis jederzeit hier auf.
Was das Kopfrechnen von Wurzeln angeht, so habe ich mich letztlich für die einfachste Ein-Schritt-Formel entschieden:
w = √a + (x - a)/(2*√a)
Wer jetzt damit beginnt, diese Formel auswendig zu lernen, wird schon bald merken, dass sie sich viel einfacher merken lässt, als man anfänglich meint. Ich demonstriere es anhand eines Beispiels: will man Wurzel 19 berechnen, nimmt man sich die nächstbeste Quadratzahl, die 16. Da Wurzel 19 zwischen Wurzel 16 (4^2) und Wurzel 25 (5^2) liegt, weiss man, dass sie vor dem Komma eine 4 haben muss, wofür die Wurzel dieser nächstbesten Quadratzahl, in diesem Fall die 16, herhält. Nun noch die Nachkommastellen, und da ist ein simpler Bruch gut - wie weit ist 19 von 16 entfernt? Genau um 3 Zahlen, das stellen wir über den Bruchstrich. Nun noch einen willkürlich klingenden Wert: das Doppelte der nächstbesten Wurzel 16, in diesem Fall also 8, stellen wir unter den Bruchstrich. Wir haben also in etwa 4 + 3/8, was man so als Lösung stehenlassen kann, wenn man den Bruch nicht in eine Dezimalzahl umwandeln möchte. Als Dezimalzahl lautet der Bruch 4,375 - die wahre Wurzel aus 19 lautet 4,3589..., womit wir diese schon sehr gut getroffen haben.
Um noch ein Beispiel zu nennen, wie ist die Wurzel aus 29? Die nächstbesten Quadratzahlen sind 25 und 36, nehmen wir hierbei einfach mal die größere - um zu zeigen, dass es damit genauso gut geht. Die Wurzel der nächsthöheren ist 6, die Zahl vor dem Komma der gesuchten Wurzel muss somit um eins niedriger sein, also 5. Wie weit is 29 von 36 entfernt? Genau, 29 ist um 7 kleiner. Nun wieder das Doppelte der Wurzel aus der nächstbesten Quadratzahl, also 2*6, das macht 12. Die Wurzel lautet also in etwa 6 + (-7)/12 oder auch 6 - 7/12, was in etwa zwischen 5,4 und 5,5 liegt. Die wahre Wurzel ist nun 5,385..., was damit zusammenhängt, dass wir eine nächstbeste Quadratzahl genommen haben, die etwas weiter entfernt war, nämlich um 7 Zahlen. Die wirklich nächste wäre die 25 gewesen, die nur um 4 Zahlen entfernt ist. Das Ergebnis damit wäre 5 + 4/10, also 5,4 - das ist ein genaueres Ergebnis, was prinzipiell einer Rundung der wahren Wurzel entspricht. Je weiter sich die nächstbeste Quadratzahl also entfernt, desto größer wird der Näherungsfehler - in den meisten Fällen jedoch sollte das zu verkraften sein, wenn man nicht gerade die ersten 100 Nachkommastellen einer Quadratwurzel exakt berechnen möchte. :-) Und in jenem Fall gibt es die bereits genannte, einfachste Quadratwurzel-Iteration der Welt mit x als für die gesuchte Wurzel stehende Variable:
Zn+1 = (Zn + x)/(Zn + 1)