chevron_left
Zurück zu "Mathematik > Hyperwürfel und -kugeln"
Weiter zu "Mathematik > Primzahlmengen II"
chevron_right10.07.2003
Primzahlmengen und Näherungen
Primzahlen sind seit Jahrtausenden ein Mysterium für Mathematiker - bislang konnten nur relativ oberflächliche Eigenschaften gefunden werden. Weder gibt es bis heute eine Formel, um die x-te Primzahl zu berechnen, noch gibt es eine exakte Möglichkeit, mit welcher man ohne Durchprobieren aller Zahlen die Anzahl der Primzahlen zwischen 1 und x berechnen kann. Selbstverständlich meine ich mit "Durchprobieren aller Zahlen" nur alle Zahlen bis x, und auch davon nur die, die auf 1, 3, 7 oder 9 enden - denn außer der 5 gibt es keine Primzahl, die auf 5 endet.
Jedoch macht die Mathematik in beiden Belangen nach und nach Fortschritte. So hat beispielsweise der Mathematiker Leonhard Euler, welcher die wohl vielseitigste mathematische Konstante e=2,71828... entdeckt hat, eine Grundlage für die Anzahl-Abschätzung von Primzahlen gelegt. Durch diese Zahl konnte später der Mathematiker Carl Friedrich Gauß herausfinden, dass die Anzahl der Primzahlen zwischen 1 und x annähernd durch den Bruch x/lnx beschrieben werden kann. LN ist der natürliche Logarithmus, also der Logarithmus zur Basis e, welcher die Umkehrfunktion zu e^x darstellt. e hoch welche Zahl ergibt x? Die Antwort lautet ln(x), vereinfacht geschrieben als lnx oder "ln x", was ausgesprochen wird als "der Logarithmus von x zur Basis e" oder "der natürliche Logarithmus von x".
Wie aber ist diese Formel x/lnx entstanden? Folgend eine kleine Tabelle. p(x) stellt dabei die Anzahl der Primzahlen bis zur Zahl x dar - hat also nichts mit der Kreiszahl p zu tun. x/p(x) ist der gerundete Faktor, der das Verhältnis zwischen Zahlen und Primzahlen bis zur Zahl x anzeigt - je größer dieser Faktor ist, desto mehr Zahlen gibt es, also desto kleiner ist der Anteil an Primzahlen. Die rechte Spalte beinhaltet jeweils die Steigung der vorletzten Spalte, von der aktuellen Zeile zur jeweils nächsten.
Der Steigungswert der rechten Spalte beginnt mit 1,5, schießt hoch bis zu 2,31, wird wieder niedriger und pendelt sich schließlich bei einer Zahl ein, die sehr an ln(10) erinnert. Aufgrund dieser Erkenntnis stellte Gauß die Vermutung auf, dass der natürliche Logarithmus mit der Anzahl der Primzahlen von 1 bis x zusammenhängt. So entstand die Formel
p(x) ~ x/lnx
Im Jahre 1808 hat dann der Mathematiker Legendre, welcher bis dato umfangreichere Daten über p(x) gesammelt hatte, die ursprüngliche Näherung noch etwas verfeinert. Seine Version lautete:
p(x) ~ x/[ln(x) - 1,08366]
Bei größer werdendem x treten sogenannte chaotische Schwingungen in der wahren Anzahl der Primzahlen auf, welche die Mathematiker möglicherweise durch die Riemann'sche Zetafunktion ausgleichen wollen, um so bessere Näherungen zu erhalten. Aus dieser Überlegung ist auch bereits eine neue Näherungsformel bekannt, welche jedoch im Verhältnis sichtbar mehr Rechenleistung benötigt als x/lnx. Die Zetafunktion, welche durch das Zeichen repräsentiert wird, besteht aus einer unendlichen Reihe, die wie folgt aussieht: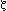
(z) = 1 + 1/(2^z) + 1/(3^z) + 1/(4^z) + ...
Die Riemann'sche Näherung zur Anzahl der Primzahlen, welche die Zeta-Funktion desselben Mathematikers enthält, lautet wie folgt:
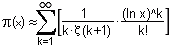
Nennen wir diese Näherung von nun an R(x), denn beide Funktionen - Näherung als auch Zeta-Funktion - wurden von Bernhard Riemann im November 1859 an die Berliner Akademie der Wissenschaft gesandt.
Ich habe nun im Mai 2003, da ich ungern bei solch faszinierenden Mathematikgebieten aufgebe, nach einigem Herumprobieren mit bisherigen Formeln und ein paar eigenen Ideen eine ähnlich genaue Variante entdeckt, welche gegenüber R(x) ein paar Vor- sowie leider auch Nachteile besitzt - bis 10^9 ist der Rechenfehler sehr gering und die Berechnung geht zügig. Bei 10^10 steigt der Fehler dann merklich an - einer der Nachteile. Ein weiterer Nachteil, um die Karten auf den Tisch zu legen, ist, dass der rechnerische Aufwand etwa ab 10^10 höher wird, als der von R(x). Zunächst nur geringfügig, bei höheren Zahlen immer merklicher. Dies ist jedoch nur dann der Fall, wenn man bei R(x) die jeweils unendlichen Reihen abbricht, sobald ein Weiterrechnen keinen sichtlichen Einfluss mehr auf das Endergebnis hat. Möchte man höhere Genauigkeit, benötigt R(x) selbstverständlich mehr Zeit, als folgende, von mir stammende Formel:
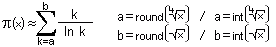
Der Anfangswert für k ist also die vierte Wurzel aus x. Diese Wurzeln nun so zu lassen wie sie ist, beeinträchtigt leider die Genauigkeit der ganzen Formel - deswegen sind die empfehlenswertesten Möglichkeiten: entweder man rundet sie auf die erste Nachkommastelle oder man ignoriert schlichtweg sämtliche Nachkommastellen. So haben wir nun unseren Startwert für k, welcher entweder gar keine oder eine einzige Nachkommastelle besitzt. Nach je einer Berechnung von k/ln(k) wird k um 1 erhöht und k/ln(k) wird mit dem nun erhöhten k ausgerechnet. Das jeweils nächste k/ln(k) wird zu allen vorherigen addiert. Sobald nach dem Addieren von 1 ein Wert bei k auftritt, der größer als die Quadratwurzel aus x ist, dann ist die Näherung fertig. Dieser Endwert sollte, wie der Startwert, auf jeden Fall ebenfalls auf die erste Nachkommastelle gerundet werden - oder man ignoriert alternativ einfach alle Nachkommastellen, ohne jegliche Rundung. Sämtliche berechnete k/ln(k) zeigen addiert nun sehr genau an, wie viele Primzahlen zwischen 1 und x existieren. Besonders stolz bin ich auf das Ergebnis 1229,03 bei x=10000, denn es gibt tatsächlich 1229 Primzahlen zwischen 1 und 10000.
Nun könnte man annehmen, dass der übrige Rechenfehler in der teilweise extremen Rundung von Startwert und Endwert liegt. Ein philosophisch begabter Freund hat mich auch darin bestärkt, da mal nachzuhaken - so kann ich nun jeden beruhigen: wenn man die gleiche Näherung ohne jegliche Rundung berechnet, ist der Fehler im Durchschnitt nicht wirklich weniger groß. Man kann jedoch etwas genauere Ergebnisse erhalten, wenn man nicht auf die Einerstelle (vor dem Komma) rundet, sondern auf die Zehntel-Stelle, also die erste Ziffer nach dem Komma. Warum das so ist, kann ich leider noch nicht wirklich beantworten - vermutlich ist die Rundung nur eine der Fehlerquellen und es gibt noch mehrere Faktoren zu bedenken, wenn man damit eine genauere Näherung erhalten möchte. Oder es ist purer Zufall :-)
Eine weitere Näherung zur Anzahl der Primzahlen ist ein logarithmisches Integral, im folgenden Li(x) genannt, welche der meinigen Näherungsversion relativ ähnlich sieht:
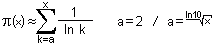
Wieder eine Formel mit dem Summenzeichen. In der allgemein bekannten Version ist der erste Wert für k restlos immer zwei, was den einfachen Hintergrund hat, dass 1/ln(k) eine nicht erlaubte Division durch 0 ergeben würde, wenn man mit 1 beginnt. Mir ist jedoch aufgefallen, dass der hierdurch errechenbare Wert immer etwas höher als die wahre Primzahl-Anzahl in dem jeweiligen Bereich ist. So habe ich etwas herumprobiert und bin schließlich bei einer Zahl gelandet, die schon ursprünglich den Mathematiker Gauß dazu bewogen hatte, den Term x/ln(x) zu verwenden: der natürliche Logarithmus von 10. Nur stellt er in diesem Fall die Wurzel von x dar, welche für den Startwert steht - wir ziehen also nicht etwa die Quadratwurzel aus x, sondern etwa die 2,3te Wurzel. Dies kann man auch schreiben als:
a = x^[1 / ln(10)]
Durch diesen neuen Startwert für Li(x) wird zwar der Gesamtaufwand nicht sehr viel weniger, welcher doch erheblich höher ist als bei meiner Variante - aber die Genauigkeit wird auf jeden Fall sichtlich gesteigert.
In der folgenden Tabelle möchte ich zeigen, wie genau oder weniger genau die bisher genannten Näherungen im Vergleich sind:
- in der ersten Spalte steht nur n, was in den Formeln in Form von 10^n verwendet wird, also die Anzahl der Nullen hinter der 1 darstellt (10^5 = 100000).
- p(10^n) stellt dabei die wahre Anzahl der Primzahlen zwischen 1 und x dar.
- L(n) steht für (10^n)/(ln(10^n) - 1,08366), das ist Legendre's Näherung für die Anzahl der Primzahlen.
- N(10^n) steht für meine Näherung, N für meinen Nachnamen Neumann, mit Zehntel-Rundung in den Startwerten.
- R(10^n) steht für die Riemann'sche Näherung.
- sämtliche Näherungen sind auf die erste Stelle VOR dem Komma gerundet, es werden also keine Nachkommastellen angezeigt.
Die erste Näherung, also die x/lnx-Variante von Légendre, ist die mit Abstand schnellste der drei genannten, denn sie beinhaltet im Vergleich nur sehr wenige Rechenschritte, selbst wenn man die Rechenoperation LN einmal ausführlich betrachtete - leider ist sie auch die ungenaueste Näherung unter den drei Formeln. Die Näherung R(x) ist ab n=8 die zweitschnellste, benötigt jedoch am meisten Speicherkapazität, da sie mit extrem hohen Zahlen rechnet. Viele allgemein zugängliche Programme sind leider nicht in der Lage zu so einer Leistung - in diesem Fall würde dann N(x) einen relativ guten Ersatz liefern. Sie ist ab n=8 zwar langsamer als R(x), rechnet dafür jedoch mit sichtbar niedrigeren Zahlen, benötigt also keine Unmengen an Speicherplatz. Ich selbst besitze leider kein Rechenprogramm, das in der Lage ist, die für R(x) nötige Genauigkeit zu erreichen, so dass ich gern die Hilfe anderer annehme. In diesem Sinne möchte ich mich herzlich bei Eugen Bauhof, Rainer Plugge und Markus M. aus dem Forum von www.wissenschaft-online.de für die Berechnungshilfe der Näherungsfunktion bedanken: Danke! :o)
Die Légendre-Näherung ist zwar perfekt geeignet um mal nebenbei einen Näherungswert zu errechnen, jedoch fällt sie jetzt aus unserer Tabelle als ungenaueste der drei Näherungen heraus. So können wir nun noch zusätzlich sehen, wie mehr oder weniger genau die zuletzt genannte Näherung Li(x) mit sowie ohne meiner kleinen Veränderung das wahre Ergebnis annähert.
Die Ursprungsversion von Li(x) ist sowohl von der Genauigkeit als auch von der Geschwindigkeit her vollkommen ungeeignet - die vorhin ausgeschlossene Näherung Légendre's würde sich eher anbieten. Die verbesserte Version von Li(x) ist bis etwa n=6 wegen der Genauigkeit gut geeignet, jedoch ist meine Näherung N(x) in jedem Fall schneller und, wie gesagt, ab n=6 fast immer genauer.
Da es mir primär um die Geschwindigkeit und Optimierung der Näherungen geht, war und bin ich sehr froh über die E-Mail von Herrn Wehmeier von der Uni Paderborn. In seiner E-Mail hat er mich u.a. darauf aufmerksam gemacht, dass meine Näherung durch ein Integral ersetzt werden kann, welches im Schnitt noch genauere Lösungen liefert. Da die dazugehörige Berechnung in fast jedem Fall sehr viel weniger Rechenleistung benötigt als meine Näherung, fühle ich mich quasi gezwungen, sie hier einzubauen und zu vergleichen. :-)
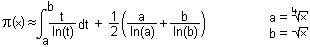
Diese Näherung, nennen wir sie Li_b(x), ist nun zwar ein wenig komplizierter, dafür jedoch bei praktischen Anwendungen wegen der höheren Rechengeschwindigkeit auf jeden Fall sinnvoller als die anderen hier genannten Näherungen.
Hier nun der Vergleich zwischen der neuen Formel Li_b(x), der Riemann'schen Näherung R(x) und meiner Näherung N(x).
Wie man hier sehen kann, kommt Li_b(x) von der durchschnittlichen Genauigkeit zwar nicht ganz an die Riemann'sche Näherung heran, welche bislang unübertroffen ist. Jedoch ist die Integral-Näherung sowohl schneller als auch zumeist genauer als meine Summen-Näherung und somit auf jeden Fall sehr viel mehr geeignet für praktische Anwendungen, sofern man jeweils praktische Anwendungen für Primzahlmengen findet... ;-)
Jedoch macht die Mathematik in beiden Belangen nach und nach Fortschritte. So hat beispielsweise der Mathematiker Leonhard Euler, welcher die wohl vielseitigste mathematische Konstante e=2,71828... entdeckt hat, eine Grundlage für die Anzahl-Abschätzung von Primzahlen gelegt. Durch diese Zahl konnte später der Mathematiker Carl Friedrich Gauß herausfinden, dass die Anzahl der Primzahlen zwischen 1 und x annähernd durch den Bruch x/lnx beschrieben werden kann. LN ist der natürliche Logarithmus, also der Logarithmus zur Basis e, welcher die Umkehrfunktion zu e^x darstellt. e hoch welche Zahl ergibt x? Die Antwort lautet ln(x), vereinfacht geschrieben als lnx oder "ln x", was ausgesprochen wird als "der Logarithmus von x zur Basis e" oder "der natürliche Logarithmus von x".
Wie aber ist diese Formel x/lnx entstanden? Folgend eine kleine Tabelle. p(x) stellt dabei die Anzahl der Primzahlen bis zur Zahl x dar - hat also nichts mit der Kreiszahl p zu tun. x/p(x) ist der gerundete Faktor, der das Verhältnis zwischen Zahlen und Primzahlen bis zur Zahl x anzeigt - je größer dieser Faktor ist, desto mehr Zahlen gibt es, also desto kleiner ist der Anteil an Primzahlen. Die rechte Spalte beinhaltet jeweils die Steigung der vorletzten Spalte, von der aktuellen Zeile zur jeweils nächsten.
| 10^n = x | p(x) | F(n) = x / p(x) | G(n) = F(n+1) - F(n) |
| 10 | 04 | 2,50 | 1,50000000 |
| 100 | 025 | 4,00 | 1,95238095 |
| 1.000 | 0.168 | 5,95 | 2,18431555 |
| 10.000 | 01.229 | 8,14 | 2,28865796 |
| 100.000 | 009.592 | 10,43 | 2,31382361 |
| 1.000.000 | 0.078.498 | 12,74 | 2,30794199 |
| 10.000.000 | 00.664.579 | 15,05 | 2,30960667 |
| 100.000.000 | 005.761.455 | 17,36 | 2,30991040 |
| 1.000.000.000 | 0.050.847.534 | 19,67 | 2,30884869 |
| 10.000.000.000 | 00.455.052.511 | 21,98 | 2,30782379 |
| 100.000.000.000 | 004.118.054.813 | 24,28 | 2,30683982 |
| 1.000.000.000.000 | 0.037.607.912.018 | 26,59 | 2,30611136 |
| 10.000.000.000.000 | 00.346.065.536.839 | 28,90 | 2,30555435 |
| 100.000.000.000.000 | 003.204.941.750.802 | 31,20 | 2,30511715 |
| ln(10) = 2,30258509 | |||
Der Steigungswert der rechten Spalte beginnt mit 1,5, schießt hoch bis zu 2,31, wird wieder niedriger und pendelt sich schließlich bei einer Zahl ein, die sehr an ln(10) erinnert. Aufgrund dieser Erkenntnis stellte Gauß die Vermutung auf, dass der natürliche Logarithmus mit der Anzahl der Primzahlen von 1 bis x zusammenhängt. So entstand die Formel
p(x) ~ x/lnx
Im Jahre 1808 hat dann der Mathematiker Legendre, welcher bis dato umfangreichere Daten über p(x) gesammelt hatte, die ursprüngliche Näherung noch etwas verfeinert. Seine Version lautete:
p(x) ~ x/[ln(x) - 1,08366]
Bei größer werdendem x treten sogenannte chaotische Schwingungen in der wahren Anzahl der Primzahlen auf, welche die Mathematiker möglicherweise durch die Riemann'sche Zetafunktion ausgleichen wollen, um so bessere Näherungen zu erhalten. Aus dieser Überlegung ist auch bereits eine neue Näherungsformel bekannt, welche jedoch im Verhältnis sichtbar mehr Rechenleistung benötigt als x/lnx. Die Zetafunktion, welche durch das Zeichen repräsentiert wird, besteht aus einer unendlichen Reihe, die wie folgt aussieht:
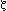(z) = 1 + 1/(2^z) + 1/(3^z) + 1/(4^z) + ...
Die Riemann'sche Näherung zur Anzahl der Primzahlen, welche die Zeta-Funktion desselben Mathematikers enthält, lautet wie folgt:
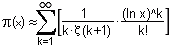
Nennen wir diese Näherung von nun an R(x), denn beide Funktionen - Näherung als auch Zeta-Funktion - wurden von Bernhard Riemann im November 1859 an die Berliner Akademie der Wissenschaft gesandt.
Ich habe nun im Mai 2003, da ich ungern bei solch faszinierenden Mathematikgebieten aufgebe, nach einigem Herumprobieren mit bisherigen Formeln und ein paar eigenen Ideen eine ähnlich genaue Variante entdeckt, welche gegenüber R(x) ein paar Vor- sowie leider auch Nachteile besitzt - bis 10^9 ist der Rechenfehler sehr gering und die Berechnung geht zügig. Bei 10^10 steigt der Fehler dann merklich an - einer der Nachteile. Ein weiterer Nachteil, um die Karten auf den Tisch zu legen, ist, dass der rechnerische Aufwand etwa ab 10^10 höher wird, als der von R(x). Zunächst nur geringfügig, bei höheren Zahlen immer merklicher. Dies ist jedoch nur dann der Fall, wenn man bei R(x) die jeweils unendlichen Reihen abbricht, sobald ein Weiterrechnen keinen sichtlichen Einfluss mehr auf das Endergebnis hat. Möchte man höhere Genauigkeit, benötigt R(x) selbstverständlich mehr Zeit, als folgende, von mir stammende Formel:
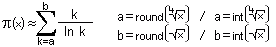
Der Anfangswert für k ist also die vierte Wurzel aus x. Diese Wurzeln nun so zu lassen wie sie ist, beeinträchtigt leider die Genauigkeit der ganzen Formel - deswegen sind die empfehlenswertesten Möglichkeiten: entweder man rundet sie auf die erste Nachkommastelle oder man ignoriert schlichtweg sämtliche Nachkommastellen. So haben wir nun unseren Startwert für k, welcher entweder gar keine oder eine einzige Nachkommastelle besitzt. Nach je einer Berechnung von k/ln(k) wird k um 1 erhöht und k/ln(k) wird mit dem nun erhöhten k ausgerechnet. Das jeweils nächste k/ln(k) wird zu allen vorherigen addiert. Sobald nach dem Addieren von 1 ein Wert bei k auftritt, der größer als die Quadratwurzel aus x ist, dann ist die Näherung fertig. Dieser Endwert sollte, wie der Startwert, auf jeden Fall ebenfalls auf die erste Nachkommastelle gerundet werden - oder man ignoriert alternativ einfach alle Nachkommastellen, ohne jegliche Rundung. Sämtliche berechnete k/ln(k) zeigen addiert nun sehr genau an, wie viele Primzahlen zwischen 1 und x existieren. Besonders stolz bin ich auf das Ergebnis 1229,03 bei x=10000, denn es gibt tatsächlich 1229 Primzahlen zwischen 1 und 10000.
Nun könnte man annehmen, dass der übrige Rechenfehler in der teilweise extremen Rundung von Startwert und Endwert liegt. Ein philosophisch begabter Freund hat mich auch darin bestärkt, da mal nachzuhaken - so kann ich nun jeden beruhigen: wenn man die gleiche Näherung ohne jegliche Rundung berechnet, ist der Fehler im Durchschnitt nicht wirklich weniger groß. Man kann jedoch etwas genauere Ergebnisse erhalten, wenn man nicht auf die Einerstelle (vor dem Komma) rundet, sondern auf die Zehntel-Stelle, also die erste Ziffer nach dem Komma. Warum das so ist, kann ich leider noch nicht wirklich beantworten - vermutlich ist die Rundung nur eine der Fehlerquellen und es gibt noch mehrere Faktoren zu bedenken, wenn man damit eine genauere Näherung erhalten möchte. Oder es ist purer Zufall :-)
Eine weitere Näherung zur Anzahl der Primzahlen ist ein logarithmisches Integral, im folgenden Li(x) genannt, welche der meinigen Näherungsversion relativ ähnlich sieht:
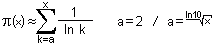
Wieder eine Formel mit dem Summenzeichen. In der allgemein bekannten Version ist der erste Wert für k restlos immer zwei, was den einfachen Hintergrund hat, dass 1/ln(k) eine nicht erlaubte Division durch 0 ergeben würde, wenn man mit 1 beginnt. Mir ist jedoch aufgefallen, dass der hierdurch errechenbare Wert immer etwas höher als die wahre Primzahl-Anzahl in dem jeweiligen Bereich ist. So habe ich etwas herumprobiert und bin schließlich bei einer Zahl gelandet, die schon ursprünglich den Mathematiker Gauß dazu bewogen hatte, den Term x/ln(x) zu verwenden: der natürliche Logarithmus von 10. Nur stellt er in diesem Fall die Wurzel von x dar, welche für den Startwert steht - wir ziehen also nicht etwa die Quadratwurzel aus x, sondern etwa die 2,3te Wurzel. Dies kann man auch schreiben als:
a = x^[1 / ln(10)]
Durch diesen neuen Startwert für Li(x) wird zwar der Gesamtaufwand nicht sehr viel weniger, welcher doch erheblich höher ist als bei meiner Variante - aber die Genauigkeit wird auf jeden Fall sichtlich gesteigert.
In der folgenden Tabelle möchte ich zeigen, wie genau oder weniger genau die bisher genannten Näherungen im Vergleich sind:
- in der ersten Spalte steht nur n, was in den Formeln in Form von 10^n verwendet wird, also die Anzahl der Nullen hinter der 1 darstellt (10^5 = 100000).
- p(10^n) stellt dabei die wahre Anzahl der Primzahlen zwischen 1 und x dar.
- L(n) steht für (10^n)/(ln(10^n) - 1,08366), das ist Legendre's Näherung für die Anzahl der Primzahlen.
- N(10^n) steht für meine Näherung, N für meinen Nachnamen Neumann, mit Zehntel-Rundung in den Startwerten.
- R(10^n) steht für die Riemann'sche Näherung.
- sämtliche Näherungen sind auf die erste Stelle VOR dem Komma gerundet, es werden also keine Nachkommastellen angezeigt.
| n | p(10^n) | L(10^n) | N(10^n) | R(10^n) |
| 1 | 4 | 8 | 6 | 4 |
| 2 | 25 | 28 | 24 | 25 |
| 3 | 168 | 172 | 170 | 167 |
| 4 | 1.229 | 1.231 | 1.229 | 1.226 |
| 5 | 9.592 | 9.588 | 9.566 | 9.586 |
| 6 | 78.498 | 78.543 | 78.469 | 78.526 |
| 7 | 664.579 | 665.140 | 664.629 | 664.666 |
| 8 | 5.761.455 | 5.768.004 | 5.761.517 | 5.761.551 |
| 9 | 50.847.534 | 50.917.518 | 50.847.417 | 50.847.554 |
| 10 | 455.052.511 | 455.743.002 | 455.043.408 | 455.050.454 |
| 11 | 4.118.054.813 | 4.124.599.873 | 4.118.039.927 | 4.118.052.541 |
| 12 | 37.607.912.018 | 37.668.527.580 | 37.607.907.918 | 37.607.910.542 |
| 13 | 346.065.536.839 | 346.621.099.395 | 346.065.447.633 | 346.065.531.065 |
| 14 | 3.204.941.750.802 | 3.210.012.053.274 | 3.204.941.276.880 | 3.204.941.731.601 |
| 15 | 29.844.570.422.669 | 29.890.794.579.819 | 29.844.570.069.567 | 29.844.570.495.886 |
Die erste Näherung, also die x/lnx-Variante von Légendre, ist die mit Abstand schnellste der drei genannten, denn sie beinhaltet im Vergleich nur sehr wenige Rechenschritte, selbst wenn man die Rechenoperation LN einmal ausführlich betrachtete - leider ist sie auch die ungenaueste Näherung unter den drei Formeln. Die Näherung R(x) ist ab n=8 die zweitschnellste, benötigt jedoch am meisten Speicherkapazität, da sie mit extrem hohen Zahlen rechnet. Viele allgemein zugängliche Programme sind leider nicht in der Lage zu so einer Leistung - in diesem Fall würde dann N(x) einen relativ guten Ersatz liefern. Sie ist ab n=8 zwar langsamer als R(x), rechnet dafür jedoch mit sichtbar niedrigeren Zahlen, benötigt also keine Unmengen an Speicherplatz. Ich selbst besitze leider kein Rechenprogramm, das in der Lage ist, die für R(x) nötige Genauigkeit zu erreichen, so dass ich gern die Hilfe anderer annehme. In diesem Sinne möchte ich mich herzlich bei Eugen Bauhof, Rainer Plugge und Markus M. aus dem Forum von www.wissenschaft-online.de für die Berechnungshilfe der Näherungsfunktion bedanken: Danke! :o)
Die Légendre-Näherung ist zwar perfekt geeignet um mal nebenbei einen Näherungswert zu errechnen, jedoch fällt sie jetzt aus unserer Tabelle als ungenaueste der drei Näherungen heraus. So können wir nun noch zusätzlich sehen, wie mehr oder weniger genau die zuletzt genannte Näherung Li(x) mit sowie ohne meiner kleinen Veränderung das wahre Ergebnis annähert.
| n | p(10^n) | Li(10^n) original | Li(10^n) verändert | N(10^n) |
| 1 | 4 | 6 | 5 | 6 |
| 2 | 25 | 30 | 25 | 24 |
| 3 | 168 | 177 | 168 | 170 |
| 4 | 1.229 | 1.246 | 1.227 | 1.229 |
| 5 | 9.592 | 9.630 | 9.590 | 9.566 |
| 6 | 78.498 | 78.627 | 78.541 | 78.469 |
| 7 | 664.579 | 664.918 | 664.727 | 664.629 |
| 8 | 5.761.455 | 5.762.209 | 5.761.769 | 5.761.517 |
| 9 | 50.847.534 | 50.849.235 | 50.848.197 | 50.847.417 |
| 10 | 455.052.511 | 455.055.614 | 455.053.122 | 455.043.408 |
| 11 | 4.118.054.813 | 4.118.066.400 | 4.118.060.329 | 4.118.039.927 |
| 12 | 37.607.912.018 | 37.607.950.281 | 37.607.935.321 | 37.607.907.918 |
| 13 | 346.065.536.839 | 346.065.645.810 | 346.065.608.612 | 346.065.447.633 |
| 14 | 3.204.941.750.802 | 3.204.942.065.692 | 3.204.941.972.500 | 3.204.941.276.880 |
| 15 | 29.844.570.422.669 | 29.844.571.475.287 | 29.844.571.240.332 | 29.844.570.069.567 |
Die Ursprungsversion von Li(x) ist sowohl von der Genauigkeit als auch von der Geschwindigkeit her vollkommen ungeeignet - die vorhin ausgeschlossene Näherung Légendre's würde sich eher anbieten. Die verbesserte Version von Li(x) ist bis etwa n=6 wegen der Genauigkeit gut geeignet, jedoch ist meine Näherung N(x) in jedem Fall schneller und, wie gesagt, ab n=6 fast immer genauer.
Da es mir primär um die Geschwindigkeit und Optimierung der Näherungen geht, war und bin ich sehr froh über die E-Mail von Herrn Wehmeier von der Uni Paderborn. In seiner E-Mail hat er mich u.a. darauf aufmerksam gemacht, dass meine Näherung durch ein Integral ersetzt werden kann, welches im Schnitt noch genauere Lösungen liefert. Da die dazugehörige Berechnung in fast jedem Fall sehr viel weniger Rechenleistung benötigt als meine Näherung, fühle ich mich quasi gezwungen, sie hier einzubauen und zu vergleichen. :-)
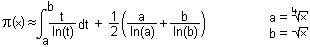
Diese Näherung, nennen wir sie Li_b(x), ist nun zwar ein wenig komplizierter, dafür jedoch bei praktischen Anwendungen wegen der höheren Rechengeschwindigkeit auf jeden Fall sinnvoller als die anderen hier genannten Näherungen.
Hier nun der Vergleich zwischen der neuen Formel Li_b(x), der Riemann'schen Näherung R(x) und meiner Näherung N(x).
| n | p(10^n) | Li_b(10^n) | R(10^n) | N(10^n) |
| 1 | 4 | 7 | 4 | 6 |
| 2 | 25 | 28 | 25 | 24 |
| 3 | 168 | 170 | 167 | 170 |
| 4 | 1.229 | 1.229 | 1.226 | 1.229 |
| 5 | 9.592 | 9.589 | 9.586 | 9.566 |
| 6 | 78.498 | 78.527 | 78.526 | 78.469 |
| 7 | 664.579 | 664.659 | 664.666 | 664.629 |
| 8 | 5.761.455 | 5.761.517 | 5.761.551 | 5.761.517 |
| 9 | 50.847.534 | 50.847.344 | 50.847.554 | 50.847.417 |
| 10 | 455.052.511 | 455.050.352 | 455.050.454 | 455.043.408 |
| 11 | 4.118.054.813 | 4.118.051.590 | 4.118.052.541 | 4.118.039.927 |
| 12 | 37.607.912.018 | 37.607.909.063 | 37.607.910.542 | 37.607.907.918 |
| 13 | 346.065.536.839 | 346.065.542.248 | 346.065.531.065 | 346.065.447.633 |
| 14 | 3.204.941.750.802 | 3.204.941.934.260 | 3.204.941.731.601 | 3.204.941.276.880 |
| 15 | 29.844.570.422.669 | 29.844.572.751.595 | 29.844.570.495.886 | 29.844.570.069.567 |
Wie man hier sehen kann, kommt Li_b(x) von der durchschnittlichen Genauigkeit zwar nicht ganz an die Riemann'sche Näherung heran, welche bislang unübertroffen ist. Jedoch ist die Integral-Näherung sowohl schneller als auch zumeist genauer als meine Summen-Näherung und somit auf jeden Fall sehr viel mehr geeignet für praktische Anwendungen, sofern man jeweils praktische Anwendungen für Primzahlmengen findet... ;-)