chevron_left
Zurück zu "Mathematik > Primzahlmengen"
Weiter zu "Mathematik > Primzahlzwillinge"
chevron_right04.12.2003
Primzahlmengen II
Ich habe mich dafür entschieden, diesen Zusatzartikel zu Primzahl-Mengen nicht als 6. Teil an den anderen "Primzahl-Mengen"-Artikel anzuhängen, da er dann vermutlich nur recht selten gelesen wird, obgleich er wichtiger ist als die dort zu findenden Näherungsformeln - zudem denke ich, dass fünf Teile für einen Artikel mehr als genug sind.
Einige Leser mögen die ursprünglichen Näherungsformeln für Primzahl-Mengen und die n-te Primzahl kennen:
1.) Zwischen 1 und n befinden sich in etwa n / ln(n) Primzahlen 2.) Die n-te Primzahl ist durchschnittlich n * ln(n)
Probiert man diese Formeln nun konsequent aus, so stellt man jedoch relativ schnell fest, dass sie für den alltäglichen Mathematikgebrauch nicht wirklich zu gebrauchen sind, denn sie werden erst bei sehr großen Zahlen genauer. Für kleinere Zahlen existieren daher weitere Näherungsformeln, welche zwar bei jenen größeren Zahlen über das Ziel hinausschießen und wieder ungenauer werden, jedoch bei "menschlichen" Zahlen sichtlich nützlicher sind. Jene Alternativen sind im ersten "Primzahl-Mengen"-Artikel zu finden.
Da die obigen Näherungen jedoch von äußerst grundlegender Natur sind, die zudem bewiesen sind, kam es mir in den Sinn, sie auf weitere Eigenschaften zu untersuchen, die in irgendeiner Form mit Primzahlen zu tun haben könnten. So kam mir zuerst die Idee, einfach mal beide gegensätzliche Näherungen miteinander zu verknüpfen - setzen wir also bei n / ln(n) einfach mal n = m * ln(m), das sieht dann so aus:
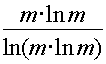
Nun fangen wir mal bei m = 5 an. Wir schauen, was die Primzahlmengen-Näherung uns sagt und verdoppeln das m dann jeweils. Folgende Tabelle kommt dabei heraus:
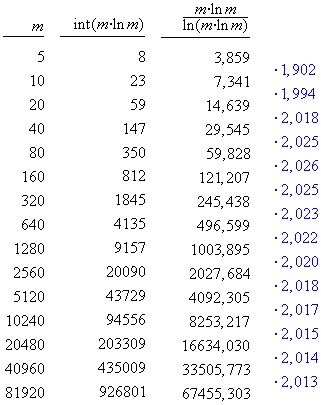
In der dritten Spalte wird durch die rechts nebenstehenden, blauen Zahlen verdeutlicht, dass sich die Anzahl der Primzahlen zwischen m * ln(m) und 2m * ln(2m) praktisch verdoppelt, von geringen Abweichungen abgesehen. Das klingt soweit noch nicht sehr spektakulär - und das ist es auch noch nicht, denn die Ergebnisse sind in diesem Zustand bei kleinen Zahlen so ungenau, wie sie es bei der Näherung n / ln(n) nun einmal sind. Der Clou liegt nun mehr darin: weiß man, wie viele Primzahlen es zwischen 1 und einer Zahl x = n * ln(n) gibt, so kann man abschätzen, dass es nahezu doppeltsoviele Primzahlen zwischen 1 und einer Zahl y = 2n * ln(2n) geben muss. Man kann auch jeden anderen Faktor an Stelle der 2 nehmen, die Genauigkeit ist trotzdem enorm. Ich zeige dies anhand einiger Beispiele in einerseits unterschiedlichen Größenordnungen und andererseits mit unterschiedlichen Faktoren.
1. Wie wir wissen, gibt es zwischen der Zahl 1 und 8 genau vier Primzahlen, nämlich 2, 3, 5 und 7. Nun müssen wir nur wissen, wie sich 8 annähernd als n * ln(n) schreiben lässt. Dafür passt 5 * ln(5) = 8,0472 recht gut. Anhand dieses Verfahrens können wir nun die Zahl 5 beispielsweise um Faktor 10 erweitern und so abschätzen, dass es zwischen 1 und der Zahl 50 * ln(50) = 195,6 rund 40 (zehn mal so viele) Primzahlen geben muss. Es existieren zwischen 1 und 195 genau 44 Primzahlen, also haben wir hier eine Abweichung von vier.
2. Zwischen den Zahlen 1 und 100 gibt es genau 25 Primzahlen. Um 100 in etwa als n * ln(n) zu schreiben, setzen wir für n einfach 30 ein - dadurch haben wir 30 * ln(30) = 102,0359. Erweitern wir die 30 nun um Faktor 3 auf 90, so können wir abschätzen, dass es zwischen 1 und 90 * ln(90) = 404,983 rund 25 * 3 = 75 Primzahlen geben müsste. Die genaue Anzahl der Primzahlen in diesem Bereich liegt bei 79, also abermals ein Schätzungsfehler von vier.
3. Im Zahlenbereich zwischen 1 und 10000 gibt es präzise 1229 Primzahlen. Um 10000 annähernd als n * ln(n) zu schreiben, schätze ich n nach 5 Versuchen auf 1390, womit wir 1390 * ln(1390) = 10059,51 haben. Verdoppeln wir die 1390 nun, so sollten zwischen 1 und 2780 * ln(2780) = 22045,97 in etwa doppeltsoviele Primzahlen liegen, also 1229 * 2 = 2458. Tatsächlich liegen zwischen 1 und 22045 genau 2471 Primzahlen, also ein Fehler von 13 in diesem Fall.
Prinzipiell könnte ich unzählige weitere Beispiele aufzeigen. Es gibt auch noch Beispiele mit größeren Fehlern, welche jedoch aufgrund entsprechend großer Zahlengrößenordnungen praktisch nicht ins Gewicht fallen. Fakt ist in jedem Fall, dass man hierbei wirklich nur grob zu schätzen braucht, wenn man wissen möchte, wie viele Zahlen nötig sind, um eine jeweils vielfache Menge an Primzahlen zu fassen. Man muss das n von n * ln(n) nur um einen beliebigen Faktor erweitern, der nicht einmal ganzzahlig zu sein braucht - schließlich erweitert man noch die bereits bekannte Anzahl der Primzahlen in einem Zahlenbereich (z.B. 25 Primzahlen zwischen 1 und 100) um denselben Faktor und hat somit eine sehr genaue Schätzung. Es ist also nicht notwendig, außergewöhnlich komplizierte Rechenoperationen durchzuführen. Lediglich einige Schätzungen. Folgend noch eine Tabelle mit weiteren Beispielen. Beachten Sie dabei, dass sich die Anzahl der Primzahlen von Zeile zu Zeile beinahe verdoppelt, abgesehen von der kleinen, offenbar chaotischen Abweichung, die immer relativ zur Anzahl von Primzahlen der jeweils darüberliegenden Zeile angegeben wird.
F(n) = int[n * ln(n)]
Einige Leser mögen die ursprünglichen Näherungsformeln für Primzahl-Mengen und die n-te Primzahl kennen:
1.) Zwischen 1 und n befinden sich in etwa n / ln(n) Primzahlen 2.) Die n-te Primzahl ist durchschnittlich n * ln(n)
Probiert man diese Formeln nun konsequent aus, so stellt man jedoch relativ schnell fest, dass sie für den alltäglichen Mathematikgebrauch nicht wirklich zu gebrauchen sind, denn sie werden erst bei sehr großen Zahlen genauer. Für kleinere Zahlen existieren daher weitere Näherungsformeln, welche zwar bei jenen größeren Zahlen über das Ziel hinausschießen und wieder ungenauer werden, jedoch bei "menschlichen" Zahlen sichtlich nützlicher sind. Jene Alternativen sind im ersten "Primzahl-Mengen"-Artikel zu finden.
Da die obigen Näherungen jedoch von äußerst grundlegender Natur sind, die zudem bewiesen sind, kam es mir in den Sinn, sie auf weitere Eigenschaften zu untersuchen, die in irgendeiner Form mit Primzahlen zu tun haben könnten. So kam mir zuerst die Idee, einfach mal beide gegensätzliche Näherungen miteinander zu verknüpfen - setzen wir also bei n / ln(n) einfach mal n = m * ln(m), das sieht dann so aus:
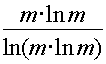
Nun fangen wir mal bei m = 5 an. Wir schauen, was die Primzahlmengen-Näherung uns sagt und verdoppeln das m dann jeweils. Folgende Tabelle kommt dabei heraus:

In der dritten Spalte wird durch die rechts nebenstehenden, blauen Zahlen verdeutlicht, dass sich die Anzahl der Primzahlen zwischen m * ln(m) und 2m * ln(2m) praktisch verdoppelt, von geringen Abweichungen abgesehen. Das klingt soweit noch nicht sehr spektakulär - und das ist es auch noch nicht, denn die Ergebnisse sind in diesem Zustand bei kleinen Zahlen so ungenau, wie sie es bei der Näherung n / ln(n) nun einmal sind. Der Clou liegt nun mehr darin: weiß man, wie viele Primzahlen es zwischen 1 und einer Zahl x = n * ln(n) gibt, so kann man abschätzen, dass es nahezu doppeltsoviele Primzahlen zwischen 1 und einer Zahl y = 2n * ln(2n) geben muss. Man kann auch jeden anderen Faktor an Stelle der 2 nehmen, die Genauigkeit ist trotzdem enorm. Ich zeige dies anhand einiger Beispiele in einerseits unterschiedlichen Größenordnungen und andererseits mit unterschiedlichen Faktoren.
1. Wie wir wissen, gibt es zwischen der Zahl 1 und 8 genau vier Primzahlen, nämlich 2, 3, 5 und 7. Nun müssen wir nur wissen, wie sich 8 annähernd als n * ln(n) schreiben lässt. Dafür passt 5 * ln(5) = 8,0472 recht gut. Anhand dieses Verfahrens können wir nun die Zahl 5 beispielsweise um Faktor 10 erweitern und so abschätzen, dass es zwischen 1 und der Zahl 50 * ln(50) = 195,6 rund 40 (zehn mal so viele) Primzahlen geben muss. Es existieren zwischen 1 und 195 genau 44 Primzahlen, also haben wir hier eine Abweichung von vier.
2. Zwischen den Zahlen 1 und 100 gibt es genau 25 Primzahlen. Um 100 in etwa als n * ln(n) zu schreiben, setzen wir für n einfach 30 ein - dadurch haben wir 30 * ln(30) = 102,0359. Erweitern wir die 30 nun um Faktor 3 auf 90, so können wir abschätzen, dass es zwischen 1 und 90 * ln(90) = 404,983 rund 25 * 3 = 75 Primzahlen geben müsste. Die genaue Anzahl der Primzahlen in diesem Bereich liegt bei 79, also abermals ein Schätzungsfehler von vier.
3. Im Zahlenbereich zwischen 1 und 10000 gibt es präzise 1229 Primzahlen. Um 10000 annähernd als n * ln(n) zu schreiben, schätze ich n nach 5 Versuchen auf 1390, womit wir 1390 * ln(1390) = 10059,51 haben. Verdoppeln wir die 1390 nun, so sollten zwischen 1 und 2780 * ln(2780) = 22045,97 in etwa doppeltsoviele Primzahlen liegen, also 1229 * 2 = 2458. Tatsächlich liegen zwischen 1 und 22045 genau 2471 Primzahlen, also ein Fehler von 13 in diesem Fall.
Prinzipiell könnte ich unzählige weitere Beispiele aufzeigen. Es gibt auch noch Beispiele mit größeren Fehlern, welche jedoch aufgrund entsprechend großer Zahlengrößenordnungen praktisch nicht ins Gewicht fallen. Fakt ist in jedem Fall, dass man hierbei wirklich nur grob zu schätzen braucht, wenn man wissen möchte, wie viele Zahlen nötig sind, um eine jeweils vielfache Menge an Primzahlen zu fassen. Man muss das n von n * ln(n) nur um einen beliebigen Faktor erweitern, der nicht einmal ganzzahlig zu sein braucht - schließlich erweitert man noch die bereits bekannte Anzahl der Primzahlen in einem Zahlenbereich (z.B. 25 Primzahlen zwischen 1 und 100) um denselben Faktor und hat somit eine sehr genaue Schätzung. Es ist also nicht notwendig, außergewöhnlich komplizierte Rechenoperationen durchzuführen. Lediglich einige Schätzungen. Folgend noch eine Tabelle mit weiteren Beispielen. Beachten Sie dabei, dass sich die Anzahl der Primzahlen von Zeile zu Zeile beinahe verdoppelt, abgesehen von der kleinen, offenbar chaotischen Abweichung, die immer relativ zur Anzahl von Primzahlen der jeweils darüberliegenden Zeile angegeben wird.
F(n) = int[n * ln(n)]
- bis F(____4) = _____5 gibt es ____3 Primzahlen
- bis F(____8) = ____16 gibt es ____6 Primzahlen (Abweichung 0)
- bis F(___16) = ____44 gibt es ___14 Primzahlen (Abweichung 2, denn 6 * 2 = 12)
- bis F(___32) = ___110 gibt es ___29 Primzahlen (Abweichung 1)
- bis F(___64) = ___266 gibt es ___56 Primzahlen (Abweichung -2)
- bis F(__128) = ___621 gibt es __114 Primzahlen (Abweichung 2)
- bis F(__256) = __1419 gibt es __223 Primzahlen (Abweichung -5)
- bis F(__512) = __3194 gibt es __452 Primzahlen (Abweichung 6)
- bis F(_1024) = __7097 gibt es __909 Primzahlen (Abweichung 5, denn 452 * 2 = 904)
- bis F(_2048) = _15615 gibt es _1820 Primzahlen (Abweichung 2)
- bis F(_4096) = _34069 gibt es _3644 Primzahlen (Abweichung 4)
- bis F(_8192) = _73817 gibt es _7286 Primzahlen (Abweichung -2)
- bis F(16384) = 158991 gibt es 14597 Primzahlen (Abweichung 25)
- bis F(32768) = 340695 gibt es 29239 Primzahlen (Abweichung 45, denn 14597 * 2 = 29194)
- bis F(____8) = ____16 gibt es ____6 Primzahlen (Abweichung 0)
- bis F(___16) = ____44 gibt es ___14 Primzahlen (Abweichung 2, denn 6 * 2 = 12)
- bis F(___32) = ___110 gibt es ___29 Primzahlen (Abweichung 1)
- bis F(___64) = ___266 gibt es ___56 Primzahlen (Abweichung -2)
- bis F(__128) = ___621 gibt es __114 Primzahlen (Abweichung 2)
- bis F(__256) = __1419 gibt es __223 Primzahlen (Abweichung -5)
- bis F(__512) = __3194 gibt es __452 Primzahlen (Abweichung 6)
- bis F(_1024) = __7097 gibt es __909 Primzahlen (Abweichung 5, denn 452 * 2 = 904)
- bis F(_2048) = _15615 gibt es _1820 Primzahlen (Abweichung 2)
- bis F(_4096) = _34069 gibt es _3644 Primzahlen (Abweichung 4)
- bis F(_8192) = _73817 gibt es _7286 Primzahlen (Abweichung -2)
- bis F(16384) = 158991 gibt es 14597 Primzahlen (Abweichung 25)
- bis F(32768) = 340695 gibt es 29239 Primzahlen (Abweichung 45, denn 14597 * 2 = 29194)